Descriptive Statistics

“Statistics is a way of reasoning, along with a collection of tools and methods, designed to help us understand the world” (De Veaux et al. 2006, A statistician and data science expert).

Descriptive Statistics is part of Statistical analysis, which is a way to understand patterns in data, mostly number-based data. It’s used by many, including scientists and businesses.

Why do we need statistical analysis, especially in machine learning? In Machine Learning, we are trying to make inferences or make predictions based on the input data. There are a lot of statistical concepts, such as Probability, Descriptive and Distribution Statistics, Bayes Theorem and many others, that helps in data understanding, pattern identification, improved prediction accuracy, and model validation to make data-driven decisions.

Let’s start with the fundamental concept, Descriptive Statistics.

Introduction to Descriptive Statistics

In Descriptive statistics, we are trying to describe the data, so without looking at all the data, we can get a summary of the data.

Types of descriptive statistics

Here we will discuss the 2 main types of descriptive statistics:

The central tendency concerns the averages of the data values.
The variability or dispersion concerns how spread out the data values are.

Measures of Central Tendency

The ‘middle’ or ‘average’ of our data is called its central tendency. This helps us find the typical data value. The three key measures of central tendency are the mean, median, and mode.

Mean

The mean, or the average, is the most used way to find the center point of a dataset. It’s like finding the balance point of our data. To calculate the mean, you add all the values and then divide by how many values there are.

What happens if we don’t use the mean?

Imagine John, who runs a bakery. Initially, he guessed how many loaves to bake each day. The result? Sometimes, he had too many leftovers; other times, he ran out of bread, leaving customers disappointed.
How does the mean solve the problem?

John started using the mean. He noted the number of loaves sold daily for a week, then divided the total sold by seven (days). This gave him the average (or ‘typical’) number of loaves his customers bought daily. Using this mean, John improved his baking plan, reducing waste and customer disappointment.

Arithmetic mean calculator

You can calculate the mean by hand or with the help of our arithmetic mean calculator below.

!pip install gradio kaleido scipy

!pip install gradio

# @title #### Arithmetic mean calculator
import gradio as gr
import numpy as np

def calculate_mean(numbers):
    numbers = [float(num) for num in numbers.split(',')]
    return np.mean(numbers)

iface = gr.Interface(
                     title="Arithmetic mean calculator",
                     fn=calculate_mean, 
                     inputs="text", 
                     outputs=gr.Label(label="Mean"),
                     examples=[['23,45,67,89'], ['12,34,56'], ['11,22,33,44,55']])
iface.launch()

In research, we often draw data from a ‘sample’—a subset of the ‘population’—to make inferences about the whole population. The ‘population’ refers to the whole set we’re interested in studying.

Population vs Sample (Source :www.scribbr.com)

These sets can be anything, not just people—objects, events, organizations, countries, species, etc.

We calculate the mean (average) of a sample and a population with similar formulas, distinguished by notation—capital letters for population, lowercase for sample.

Population mean ($\bar{X}$ or μ)

\[\bar{X} = \dfrac{\sum X}{N}\]

where $\sum X$ is the sum of all values and $N$ is the number of values in the population.
Sample mean ($\bar{x}$ or M)

\[\bar{x} = \dfrac{\sum x}{n}\]

where $\sum x$ is the sum of all sample values and $n$ is the number of values in the sample.

Calculating the Mean: An Example

Let’s calculate the mean number of loaves of bread sold daily in a bakery over a week.

Sample data: - $x$ Number of loaves sold daily: 72, 64, 78, 84, 70, 76, 82

First, add up all the values:

\[\sum x = 72 + 64 + 78 + 84 + 70 + 76 + 82 = 526\]

Next, divide the total by the number of values (7):

\[\bar{x} = \dfrac{\sum x}{n} = \dfrac{526}{7} = 75.14\]

So, on average, approximately 75 loaves of bread are sold daily. This average can help the bakery to better forecast demand, reduce waste, and improve customer satisfaction.

Now, What’s the role of the mean in machine learning?

Much like in John’s bakery, machine learning algorithms use the mean for making accurate predictions. Without the mean, they would lack a critical reference point, leading to less accurate predictions. 🎯

Interactive chart Mean

You can explore various different data to get the mean value and learn how the mean value is positioned from our tool below.

!pip install -U gradio kaleido

# @title #### Calculate mean and plot bar chart
import warnings
warnings.filterwarnings('ignore', category=UserWarning, module='gradio')
import plotly.graph_objects as go
import gradio as gr
import plotly.io as pio
from PIL import Image
import io

# Function to calculate mean and plot bar chart
def interactive_plot(num_days, day1=0, day2=0, day3=0, day4=0, day5=0, day6=0, day7=0, sort_data=False):
    num_days = int(num_days)  # Convert num_days to integer
    days = [day1, day2, day3, day4, day5, day6, day7][:num_days]
    days_names = ['day1', 'day2', 'day3', 'day4', 'day5', 'day6', 'day7'][:num_days]

    if sort_data:
        days, days_names = zip(*sorted(zip(days, days_names), key=lambda pair: pair[0]))

    # Calculate the mean
    mean_day = sum(days) / len(days)

    # Create a bar chart
    fig = go.Figure(data=go.Bar(y=days, x=days_names, name='days'))

    # Add a horizontal line for the mean
    fig.add_trace(go.Scatter(
        x=[days_names[0], days_names[-1]],
        y=[mean_day, mean_day],
        mode='lines',
        name=f'Mean: {mean_day:.2f}',
        line=dict(color='Red', width=1, dash='dash')
    ))

    # Add labels for x and y axis
    fig.update_layout(
        xaxis_title="Days",
        yaxis_title="Number of loaves sold",
        font=dict(
            size=14,
        ),
        legend=dict(
            yanchor="top",
            y=1.2,
            xanchor="center",
            x=0.5
        )
    )

    # Convert the figure to PNG image
    png_image = pio.to_image(fig, format='png')

    # Create a PIL Image object for Gradio Output
    image = Image.open(io.BytesIO(png_image))

    return image

# Create Gradio interface
iface = gr.Interface(
    title='Interactive Mean Plot Mean',
    description='Interactive plot of the mean of 7 days',
    live=True, 
    fn=interactive_plot, 
    inputs=[
        gr.Dropdown(choices=[1, 2, 3, 4, 5, 6, 7], label="Number of days to use", value="7"),
        gr.Slider(minimum=0, maximum=100, step=1, value=72),
        gr.Slider(minimum=0, maximum=100, step=1, value=64),
        gr.Slider(minimum=0, maximum=100, step=1, value=78),
        gr.Slider(minimum=0, maximum=100, step=1, value=84),
        gr.Slider(minimum=0, maximum=100, step=1, value=70),
        gr.Slider(minimum=0, maximum=100, step=1, value=76),
        gr.Slider(minimum=0, maximum=100, step=1, value=82),
        gr.Checkbox(label="Sort data")
    ], 
    outputs=gr.Image(type='pil'),
    examples=[
        [7, 30, 35, 40, 45, 80, 90, 100], # Weekend Surge
        [7, 80, 75, 30, 35, 75, 85, 90], # Midweek Drop
        [7, 50, 70, 30, 90, 60, 40, 80], # Random Distribution
        [7, 10, 20, 30, 40, 50, 60, 70], # Constant Growth
        [7, 70, 60, 50, 40, 30, 20, 10], # Constant Decline
    ]
)

iface.launch();

Caution When Using the Mean

The mean is a common measure of central tendency, but it isn’t always the best choice. In certain situations, the mean can be misleading as it may be ‘pulled’ towards extreme values.

For example, consider a company that has 9 employees who earn between \$10,000 to \$20,000 per year, with the exception of the CEO who earns \$1,000,000. The median salary is \$113,700, which does not accurately represent the typical salary in this case.

Why? Because the CEO’s salary is very large compared to other employees, the average salary is very high and does not reflect the salary of ordinary employees.

# @title #### Calculate mean and plot bar chart
import plotly.graph_objects as go

# Define the data
salaries = [1000000, 13000, 19000, 10000, 18000, 16000, 13000, 19000, 10000, 19000]
employee_names = ['CEO', 'Employee 1', 'Employee 2', 'Employee 3', 'Employee 4', 'Employee 5', 'Employee 6', 'Employee 7', 'Employee 8', 'Employee 9']

# Calculate the mean
mean_salary = sum(salaries) / len(salaries)

# Create a bar chart
fig = go.Figure(data=go.Bar(y=salaries, x=employee_names, name='Salaries'))

# Add a horizontal line for the mean
fig.add_trace(go.Scatter(
    x=[employee_names[0], employee_names[-1]],
    y=[mean_salary, mean_salary],
    mode='lines',
    name=f'Mean: {mean_salary:.2f}',
    line=dict(color='Red', width=1, dash='dash')
))

# Add labels for x and y axis
fig.update_layout(
    xaxis_title="Employees",
    yaxis_title="Salary",
    font=dict(
        size=14,
    ),
    legend=dict(
        yanchor="top",
        y=1.2,
        xanchor="center",
        x=0.5
    )
)

# Show the plot
fig.show()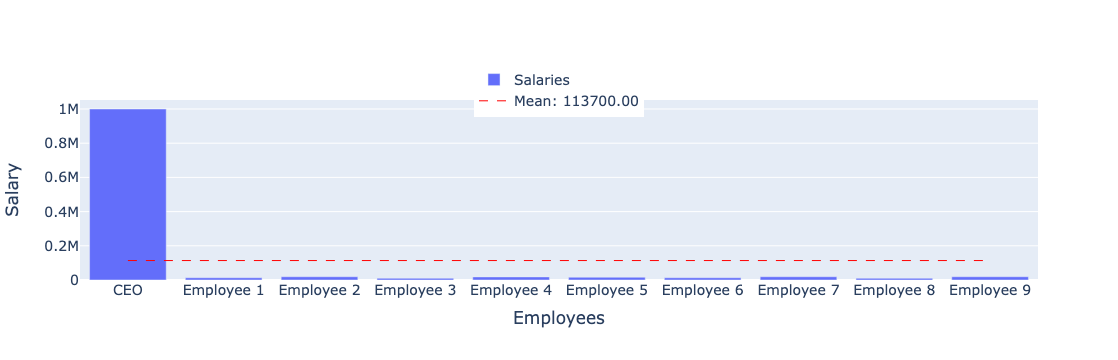

A potential solution in such cases could be to use the Median instead.

Median

What is a median? This is the middle value in a dataset once it’s sorted in order either descending or ascending. If the dataset has an even number of values, the median is the mean of the two middle numbers.

What happens if we don’t use the median?

Take for example John, a baker. John wants to establish a reliable baking plan based on the number of loaves he sells each day. Using the average (mean) in calculating daily sales can be misleading, because extreme sales (for example 1000 loaves on a festival day or 10 loaves on a rainy day) can disrupt the calculations and plans.
How does the median solve the problem?

By using the median, John gets a more stable picture of ‘typical’ daily sales, without being influenced by sales extremes, so his production plans are more reliable and efficient.

Median calculator

You can calculate the median by hand or with the help of our median calculator below.

# @title #### Median calculator
import gradio as gr
import numpy as np

def calculate_median(numbers):
    numbers = [float(num) for num in numbers.split(',')]
    return np.median(numbers)

iface = gr.Interface(fn=calculate_median, 
                     inputs="text", 
                     outputs=gr.Label(label="Median"),
                     examples=[['23,45,67,89'], ['12,34,56'], ['11,22,33,44,55']])
iface.launch()

Steps for calculating the median by hand

Let’s consider some examples from the daily bread sales at a bakery.

Odd Number of Data Points

If we track daily sales over 7 days: [72, 64, 78, 84, 70, 76, 82], and arrange the values in ascending order, the median is the middle value, which is 76.
Even Number of Data Points

If we track daily sales over 8 days: [72, 64, 78, 84, 70, 76, 82, 88], and sort the values, the median is the mean of the two middle values. This equates to (76+78)/2 = 77.

Why choose the median over the mean? The median is the central value of a data set, undistorted by outliers or skewness, making it a more accurate measure of central tendency for skewed data. After understanding the concept of the median, it’s vital to identify any outliers in our dataset as these can skew the data distribution. So, what are outliers and skewness?

Outliers are values that are significantly different from others in the dataset. They can excessively influence the mean, leading to a deceptive representation of the data.

Outliers can be detected using the Interquartile Range (IQR). Here’s how:

Take for instance, the dataset: {1, 2, 3, 4, 4, 5, 100}
1. Q1 (First Quartile): This is the median of the lower half of the dataset, which in this case is {1, 2, 3} = 2.
2. Q2 (Second Quartile or Median): This is the middle value of the full dataset, which is = 4.
3. Q3 (Third Quartile): This is the median of the upper half of the dataset, which in this case is {4, 5, 100} = 5.
4. IQR (Interquartile Range) = $Q3 - Q1$ = $5 - 2$ = 3.
5. Lower Limit: This is calculated as $Q1 - 1.5*IQR$ = $2 - 1.5*3$ = -2.5.
6. Upper Limit: This is calculated as $Q3 + 1.5*IQR$ = $5 + 1.5*3$ = 9.5.
Any value below -2.5 or above 9.5 is considered an outlier. Therefore, in this dataset 100 is an outlier.

Outliers

Outliers in a box plot (Source: whatissixsigma.net)
Skewness is an asymmetry in a dataset’s distribution. When the right tail (higher values) is longer or fatter, we have positive skewness, and the mean typically exceeds the median. Conversely, negative skewness implies a longer or fatter left tail (lower values), with the mean usually less than the median.

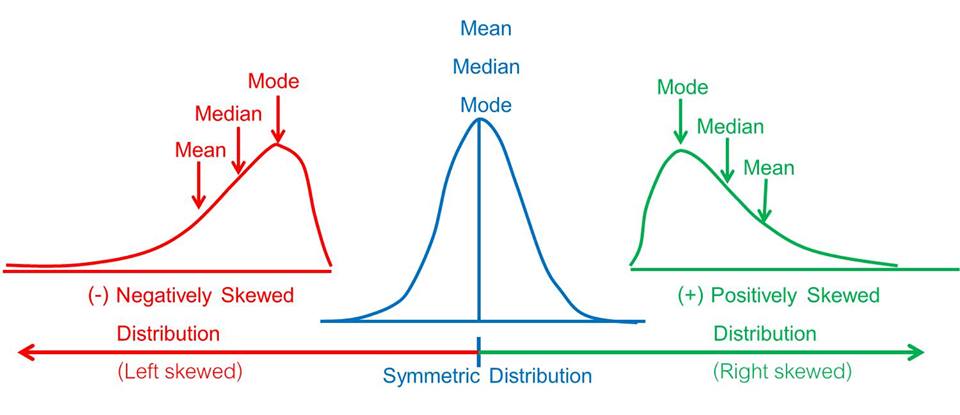
Skewness

Skewness (Source: deepai.org)

Skewness is crucial to consider as it can mislead data interpretation. For instance, in a positively skewed distribution, the mean could overestimate the typical value, making the median a more accurate measure of central tendency.

Consider a company where all 9 employees earn between \$10,000 to \$20,000 per year, with the exception of the CEO who earns \$1,000,000. In this scenario, the salary distribution exhibits positive skewness, because the CEO’s high salary pulls the average up, making the median (middle salary) a better representative of the typical salary within the company.

If we were to consider a situation where most employees earn high salaries, but a few earn significantly less (negative skewness), the median salary would still provide a more accurate representation as it would be higher than the average, which is pulled down by the few low salaries.

Thus, in skewed salary data, the median is a more reliable and representative measure of central tendency.

# @title #### Calculate mean, median and plot bar chart
import plotly.graph_objects as go
import statistics

# Define the data
salaries = [1000000, 13000, 19000, 10000, 18000, 16000, 13000, 19000, 10000, 19000]
employee_names = ['CEO', 'Employee 1', 'Employee 2', 'Employee 3', 'Employee 4', 'Employee 5', 'Employee 6', 'Employee 7', 'Employee 8', 'Employee 9']

# Calculate the mean
mean_salary = sum(salaries) / len(salaries)

# Calculate the median
median_salary = statistics.median(salaries)

# Create a bar chart
fig = go.Figure(data=go.Bar(y=salaries, x=employee_names, name='Salaries'))

# Add a horizontal line for the mean
fig.add_trace(go.Scatter(
    x=[employee_names[0], employee_names[-1]],
    y=[mean_salary, mean_salary],
    mode='lines',
    name=f'Mean: {mean_salary:.2f}',
    line=dict(color='Red', width=1, dash='dash')
))

# Add a horizontal line for the median
fig.add_trace(go.Scatter(
    x=[employee_names[0], employee_names[-1]],
    y=[median_salary, median_salary],
    mode='lines',
    name=f'Median: {median_salary:.2f}',
    line=dict(color='Blue', width=1, dash='dash')
))

# Add labels for x and y axis
fig.update_layout(
    xaxis_title="Employees",
    yaxis_title="Salary",
    font=dict(
        size=14,
    ),
    legend=dict(
        yanchor="top",
        y=1.2,
        xanchor="center",
        x=0.5
    )
)

# Show the plot
fig.show()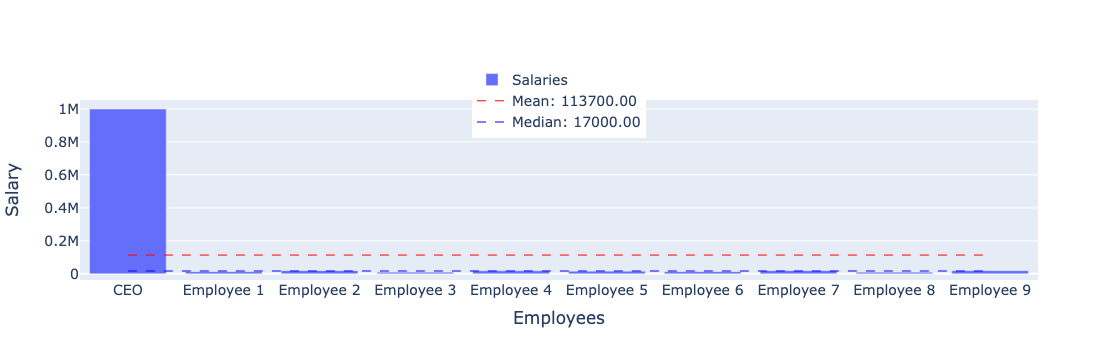

Now, What’s the role of the median in machine learning?

In machine learning, the median can sometimes be a better choice than the mean, especially when dealing with outliers (extremely high or low values) in the dataset. Using the median can help avoid this distortion and provide more reliable predictions. 🎯

Interactive chart median

You can explore various different data to get the median value and learn how the mean value is positioned from our tool below.

# @title #### Calculate mean, median and plot bar chart
import warnings
warnings.filterwarnings('ignore', category=UserWarning, module='gradio')
import numpy as np
import statistics

# Function to calculate mean, median and plot bar chart
def interactive_plot(num_days, day1=0, day2=0, day3=0, day4=0, day5=0, day6=0, day7=0, day8=0, statistics_to_show=None, sort_data=False):
    num_days = int(num_days)  # Convert num_days to integer
    days = [day1, day2, day3, day4, day5, day6, day7, day8][:num_days]
    days_names = ['day1', 'day2', 'day3', 'day4', 'day5', 'day6', 'day7', 'day8'][:num_days]

    # Sort the data if the option is selected
    if sort_data:
        days, days_names = zip(*sorted(zip(days, days_names), key=lambda pair: pair[0]))
    
    fig = go.Figure(data=go.Bar(y=days, x=days_names, name='days'))

    if 'mean' in statistics_to_show:
        # Calculate the mean
        mean_day = np.mean(days)

        # Add a horizontal line for the mean
        fig.add_trace(go.Scatter(
            x=[days_names[0], days_names[-1]],
            y=[mean_day, mean_day],
            mode='lines',
            name=f'Mean: {mean_day:.2f}',
            line=dict(color='Red', width=1, dash='dash')
        ))

    if 'median' in statistics_to_show:
        # Calculate the median
        median_day = statistics.median(days)

        # Add a horizontal line for the median
        fig.add_trace(go.Scatter(
            x=[days_names[0], days_names[-1]],
            y=[median_day, median_day],
            mode='lines',
            name=f'Median: {median_day:.2f}',
            line=dict(color='Green', width=1, dash='dash')
        ))

    # Add labels for x and y axis
    fig.update_layout(
        xaxis_title="Days",
        yaxis_title="Number of loaves sold",
        font=dict(
            size=14,
        ),
        legend=dict(
            yanchor="top",
            y=0.99,
            xanchor="left",
            x=0.01
        )
    )

    # Convert the figure to PNG image
    png_image = pio.to_image(fig, format='png')

    # Create a PIL Image object for Gradio Output
    image = Image.open(io.BytesIO(png_image))

    return image


# Create Gradio interface
iface = gr.Interface(
    title='Interactive Mean and Median Plot',
    description='Interactive plot of the mean and median number of 8 days',
    live=True,
    fn=interactive_plot, 
    inputs=[
        gr.Dropdown(choices=[1, 2, 3, 4, 5, 6, 7, 8], label="Number of days to use", value="8"),
        gr.Slider(minimum=0, maximum=100, step=1, value=64),
        gr.Slider(minimum=0, maximum=100, step=1, value=70),
        gr.Slider(minimum=0, maximum=100, step=1, value=72),
        gr.Slider(minimum=0, maximum=100, step=1, value=76),
        gr.Slider(minimum=0, maximum=100, step=1, value=78),
        gr.Slider(minimum=0, maximum=100, step=1, value=82),
        gr.Slider(minimum=0, maximum=100, step=1, value=84),
        gr.Slider(minimum=0, maximum=100, step=1, value=88),
        gr.CheckboxGroup(choices=['mean', 'median'], value=['median'], label="Statistics to show"),
        gr.Checkbox(label="Sort data")
    ], 
    outputs=gr.Image(type='pil'),
)

iface.launch()

Mode

After discussing the mean and median, another measure of central tendency we should consider is the mode. The mode is the value that appears most frequently in a dataset, and unlike the mean and median, it can be used with categorical data.

What happens if we don’t use the mode?

Imagine John, a baker. He wants to identify the most preferred type of loaf among his customers. However, without using any statistical method to analyze his sales data, he might fail to accurately identify the most sought-after loaf.
How does the mode solve the problem?

John decides to use the mode. He tallies up the types of loaves he sold within a month. The type of loaf with the highest count is the mode. This informs him of the most popular loaf type among his customers.

Mode calculator

You can calculate the mode by hand or with the help of our mode calculator below.

!pip install -U gradio scipy

# @title #### Mode calculator
import gradio as gr
from scipy import stats

def calculate_mode(numbers):
    numbers = [float(num) for num in numbers.split(',')]
    mode = stats.mode(numbers)
    return mode.mode[0]

iface = gr.Interface(fn=calculate_mode, 
                     inputs="text", 
                     outputs=gr.Label(label="Mode"),
                     examples=[['23,45,67,89,45'], ['12,34,56,34'], ['11,22,33,44,55,55']])
iface.launch()

Steps for Calculating the Mode by Hand

The ‘mode’ is the most frequently occurring value in a dataset. It’s useful when we want to find the most common value, and it’s applicable to both numerical and categorical data.

Let’s consider some examples from a bakery.

Numerical Data Example

If we track daily bread sales for 10 days: [72, 76, 72, 84, 70, 76, 76, 82, 70, 84], and tally up the frequency of each number of sales, 76 is the mode because it appears the most (3 times).
Categorical Data Example

If we track the type of pastry sold most over 10 days: [Croissant, Baguette, Baguette, Croissant, Croissant, Baguette, Sourdough, Sourdough, Croissant, Baguette], both Croissant and Baguette are modes because they appear the most (4 times each).
Grouped Data Example

Let’s say we group bread sales into intervals (60-70, 70-80, 80-90, 90-100) and record the frequency of sales falling into each group over a month. If the frequencies are 5, 7, 9, 3 respectively, the mode is the group with the highest frequency, which is 80-90.

The mode is easy to understand and calculate, and it gives us valuable insights about the most typical or common value in our dataset.

Now, What’s the role of the mode in machine learning?

In machine learning, the mode is used for categorical data. It helps identify the most common category in a dataset. Just like John’s loaf types, knowing the mode can help the model predict the most likely outcome based on past data. 🎯

To see the problem and solution in the context of using fashion, let’s go back to the example of John the baker. For example, we have data on sales of different types of bread for one month, and we want to know what type of bread is the most popular.

# @title #### Calculate mode and plot bar chart
import plotly.graph_objects as go
from collections import Counter
import pandas as pd

# Define the data
loaf_types = ['Croissant', 'Baguette', 'Baguette', 'Croissant', 'Baguette', 'Croissant', 'Baguette', 'Sourdough', 'Sourdough', 'Croissant', 'Baguette']
loaf_counts = Counter(loaf_types)

# Calculate the mode
mode_loaf = max(loaf_counts, key=loaf_counts.get)

# Create a bar chart
fig = go.Figure(data=go.Bar(y=list(loaf_counts.values()), x=list(loaf_counts.keys()), name='Loaf Types'))

# Add a horizontal line for the mode
fig.add_trace(go.Scatter(
    x=[mode_loaf, mode_loaf],
    y=[0, max(loaf_counts.values())],
    mode='lines',
    name=f'Mode: {mode_loaf}',
    line=dict(color='Red', width=1, dash='dash')
))

# Add labels for x and y axis
fig.update_layout(
    xaxis_title="Loaf Types",
    yaxis_title="Frequency",
    font=dict(
        size=14,
    ),
    legend=dict(
        yanchor="top",
        y=1.2,
        xanchor="center",
        x=0.5
    )
)

# Show the plot
fig.show()

# Convert to pandas DataFrame
df = pd.DataFrame(loaf_types, columns=["Loaf Type"])

# Group by loaf types and count the frequency
df.groupby("Loaf Type").size().reset_index(name='Counts')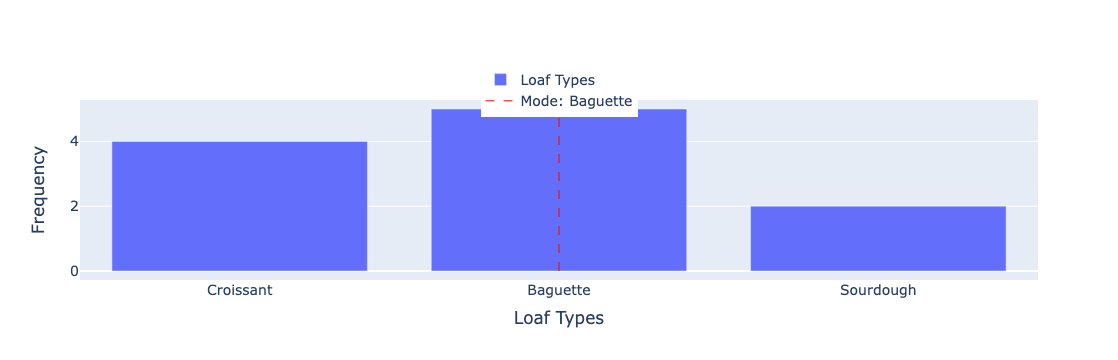

	Loaf Type	Counts
0	Baguette	5
1	Croissant	4
2	Sourdough	2

In this plot, the red line shows the mode i.e. the type of bread that is most frequently sold. The bar chart shows the frequency of sales of each type of bread, so we can see that fashion does reflect the most popular types of bread.

Interactive chart mode

You can explore various different data to get the mode value and learn how the mean value is positioned from our tool below.

# @title #### Calculate mean, median, mode and plot bar chart
import warnings
warnings.filterwarnings('ignore', category=UserWarning, module='gradio')
from scipy import stats

# Function to calculate mean, median, mode and plot bar chart
def interactive_plot(num_days, day1=0, day2=0, day3=0, day4=0, day5=0, day6=0, day7=0, day8=0, day9=0, day10=0, statistics_to_show=None, sort_data=False):
    num_days = int(num_days)  # Convert num_days to integer
    days = [day1, day2, day3, day4, day5, day6, day7, day8, day9, day10][:num_days]
    days_names = ['day1', 'day2', 'day3', 'day4', 'day5', 'day6', 'day7', 'day8', 'day9', 'day10'][:num_days]

    # Sort the data if the option is selected
    if sort_data:
        days, days_names = zip(*sorted(zip(days, days_names), key=lambda pair: pair[0]))
    
    fig = go.Figure(data=go.Bar(y=days, x=days_names, name='days'))

    if 'mean' in statistics_to_show:
        # Calculate the mean
        mean_day = np.mean(days)

        # Add a horizontal line for the mean
        fig.add_trace(go.Scatter(
            x=[days_names[0], days_names[-1]],
            y=[mean_day, mean_day],
            mode='lines',
            name=f'Mean: {mean_day:.2f}',
            line=dict(color='Red', width=1, dash='dash')
        ))

    if 'median' in statistics_to_show:
        # Calculate the median
        median_day = statistics.median(days)

        # Add a horizontal line for the median
        fig.add_trace(go.Scatter(
            x=[days_names[0], days_names[-1]],
            y=[median_day, median_day],
            mode='lines',
            name=f'Median: {median_day:.2f}',
            line=dict(color='Green', width=1, dash='dash')
        ))

    if 'mode' in statistics_to_show:
        # Calculate the mode
        mode_day = stats.mode(days)[0][0]

        # Add a horizontal line for the mode
        fig.add_trace(go.Scatter(
            x=[days_names[0], days_names[-1]],
            y=[mode_day, mode_day],
            mode='lines',
            name=f'Mode: {mode_day:.2f}',
            line=dict(color='Blue', width=1, dash='dash')
        ))

    # Add labels for x and y axis
    fig.update_layout(
        xaxis_title="days",
        yaxis_title="Number of loaves sold",
        font=dict(
            size=14,
        ),
        legend=dict(
            yanchor="top",
            y=0.99,
            xanchor="left",
            x=0.01
        )
    )

    # Convert the figure to PNG image
    png_image = pio.to_image(fig, format='png')

    # Create a PIL Image object for Gradio Output
    image = Image.open(io.BytesIO(png_image))

    return image


# Create Gradio interface
iface = gr.Interface(
    title='Interactive Plot Mean, Median, Mode and Bar Chart',
    live=True,
    fn=interactive_plot, 
    inputs=[
        gr.Dropdown(choices=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10], label="Number of days to use", value="10"),
        gr.Slider(minimum=0, maximum=100, step=1, value=72),
        gr.Slider(minimum=0, maximum=100, step=1, value=76),
        gr.Slider(minimum=0, maximum=100, step=1, value=72),
        gr.Slider(minimum=0, maximum=100, step=1, value=84),
        gr.Slider(minimum=0, maximum=100, step=1, value=70),
        gr.Slider(minimum=0, maximum=100, step=1, value=76),
        gr.Slider(minimum=0, maximum=100, step=1, value=76),
        gr.Slider(minimum=0, maximum=100, step=1, value=82),
        gr.Slider(minimum=0, maximum=100, step=1, value=70),
        gr.Slider(minimum=0, maximum=100, step=1, value=84),
        gr.CheckboxGroup(choices=['mean', 'median', 'mode'], value=['mode'], label="Statistics to show"),
        gr.Checkbox(label="Sort data")
    ], 
    outputs=gr.Image(type='pil'),
)

iface.launch()

Measures of Variability

As we delve deeper into our data, we find measures that show how spread out or diverse our data is. These are called measures of variability and include elements like the range and standard deviation. Each of these measures provides a unique perspective on how scattered the values in our data are.

Range

What is range? This is the difference between the highest and lowest values in a dataset. In other words, it measures the spread or the dispersion of the data points in a dataset.

Why use the range?
- Simplicity: The range is one of the simplest forms of statistical analysis. It provides a quick, easy-to-understand measure of dispersion in a dataset.
- Identify Spread: The range can provide an initial sense of how spread out the numbers in the dataset are. It gives a rough overview of the dispersion of the data.
- Outliers Detection: It can also be useful in some cases for highlighting outliers. An unusually large range can signify that there may be outlier values in the dataset.

However, it is important to note that the range only considers the two extreme values in the dataset and does not take into account any of the other values in the dataset. This means it can be heavily influenced by outliers and may not accurately represent the dispersion for all datasets, especially those with extreme values. For a more robust measure of dispersion, consider using other statistics, such as standard deviation.

Range calculator

You can calculate the range by hand or with the help of our range calculator below.

# @title #### Range calculator
import gradio as gr

def calculate_range(numbers):
    numbers = [float(num) for num in numbers.split(',')]
    range_value = max(numbers) - min(numbers)
    return range_value

iface = gr.Interface(fn=calculate_range, 
                     inputs="text", 
                     outputs=gr.Label(label="Range"),
                     examples=[['23,45,67,89'], ['12,34,56'], ['11,22,33,44,55']])
iface.launch()

Understanding the Significance and Calculation of Range

Before diving into the mechanical aspect of calculating the range, it’s essential to understand its fundamental role.

Range is a statistical measure that provides insights into the spread of your data. It helps us comprehend the variability within the dataset and gives us a handle on the extent of potential prediction outputs. This understanding ultimately contributes to making more accurate forecasts in machine learning models. 🎯

Now, intuitively, to gauge how spread out your data is, you’d want to consider the two extreme points - the highest and the lowest values. The greater the difference between these two, the larger is the spread, and hence, the bigger the range.

With this intuitive understanding, let’s formalize the concept:

To calculate the range, you indeed follow these steps:

Arrange your data from low to high.
Deduct the lowest value from the highest value.

These steps can be summarized in the formula:

\[Range = Highest - Lowest\]

Let’s apply this to an example:

Example Data: - Daily bread sales: 72, 64, 78, 84, 70, 76, 82

Firstly, arrange the data:

Ordered sales: 64, 70, 72, 76, 78, 82, 84

Applying the formula gives us the range:

Range = 84 - 64

So, in our example, the range is 20 loaves. This tells us about the spread in daily bread sales but does not provide information on how sales are distributed within this range. Yet, it provides a quick overview of the data spread.

Caution on the use of Range

While range is very easy to calculate and can be a good indicator of data spread, just like the Mean, if we have one very big value or very small value (outliers), then the range will not reflect the data accurately.

Let’s say from the Daily bread sales above, there is one day where the sales of bread that day is 150, out data becomes: > - Daily bread sales: 72, 64, 78, 84, 70, 76, 82, 150

Using the formula for Range:

Range = 150 - 64 = 86

Clearly 86 is a big jump compared to the previously calculated range of 20 loaves.

Standard Deviation

This is where Standard Deviation comes in, it measures the average distance your data values are from the Mean. This is crucial as it provides a gauge of how much the data varies and how reliable the average is in representing the data.

For instance, consider five individuals who might have the following amounts of money in their wallets: \$21, \$50, \$62, \$85, \$90. The mean (average) amount is \$61.60 and the standard deviation is 28.01.

This means that the spread is 28.01 to the right of the Mean (\$61.60) and also 28.01 to the left. Note that it does not match exactly the highest (\$90 vs \$89.61) and the lowest value (\$21 vs \$33.59).

The formal formula for standard deviation is as follows:

For a population:

\[\sigma =\sqrt{\frac{\sum{(X - \mu)^2}}{N}}\]
For a sample:

\[s =\sqrt{\frac{\sum{(X - \bar{x})^2}}{n - 1}}\]

The distinguishing factor between the sample and population formulas lies in the denominator. For a sample, we utilize n - 1 (known as the Bessel’s correction) as the divisor, rather than N. This technique is implemented to correct for bias in the estimation of the population variance, providing a more conservative estimate.

So, how do we calculate this in practice? Let’s illustrate this with an example of a dataset comprising six test scores to find the standard deviation:

Data set: $46, 69, 32, 60, 52, 41$

Calculate the Mean (Average): This is the central point of our data. We need the mean as a reference point to measure how much our data varies.

Why? The mean serves as the central value of our dataset, and we measure the variation of our data based on how far these values deviate from this central point.

Let’s calculate the mean for our dataset:

\[\mu = \frac{\sum{X}}{N} = \frac{46 + 69 + 32 + 60 + 52 + 41}{6} = 50\]
Calculate the Difference of Each Value from the Mean: This is the distance of each data point from the mean.

Why? We want to know how far each data point is from the average. The further a data point is from the average, the higher the variability.

Let’s calculate the differences:

\[\begin{align*} 46 - 50 &= -4 \\ 69 - 50 &= 19 \\ 32 - 50 &= -18 \\ 60 - 50 &= 10 \\ 52 - 50 &= 2 \\ 41 - 50 &= -9 \end{align*}\]
Square the Differences: We take the absolute value of the differences by squaring them.

Why? There are two main reasons.
- First, this ensures all difference values are positive (since the square of a negative number is positive).
  - Why? This is useful as summing differences without squaring could negate positive and negative divergences, falsely implying no variance when there actually is.
- Second, it gives more weight to values that are further from the mean.
  - Why? As the square of a larger number is much greater than a smaller one’s, larger deviations from the mean significantly affect variance or standard deviation values. This emphasizes the presence of outliers, or values notably different from the mean, in your data.
Let’s square the differences:

\[\begin{align*} (-4)^2 &= 16 \\ (19)^2 &= 361 \\ (-18)^2 &= 324 \\ (10)^2 &= 100 \\ (2)^2 &= 4 \\ (-9)^2 &= 81 \end{align*}\]

import plotly.express as px
import pandas as pd
import numpy as np
import plotly.graph_objs as go

# Create a DataFrame with your data
df = pd.DataFrame({
    'Test Scores': [46, 69, 32, 60, 52, 41]
})

# Calculate the mean
mean = df['Test Scores'].mean()

# Calculate the deviations
df['Deviation'] = df['Test Scores'] - mean

# Calculate the squared deviations
df['Squared Deviations'] = np.square(df['Deviation'])

# Create a bar chart of squared deviations
fig = px.bar(df, x='Test Scores', y='Squared Deviations', 
             title='Squared Deviations of Test Scores',
             labels={'Squared Deviations': 'Squared Deviations', 'Test Scores': 'Test Scores'})

# Add an invisible trace for mean, just for the sake of legend
fig.add_trace(go.Scatter(
    x=[df['Test Scores'].min(), df['Test Scores'].max()],
    y=[mean, mean],
    mode="lines",
    line=go.scatter.Line(color="rgba(0,0,0,0)"),  # Transparent color
    showlegend=True,
    name="Mean Test Scores: {:.2f}".format(mean),  # Show mean value in the legend
))

fig.show()

Unable to display output for mime type(s): application/vnd.plotly.v1+json

Average the Squared Differences: Now we calculate the average of all these squared difference values.

Why? We want to know on average how spread out our data is. If we were to just sum these values, larger datasets would appear to have higher spreads. By taking the average, we normalize it.

Let’s calculate the average:

\[\frac{\sum{(X - \mu)^2}}{N} = \frac{16 + 361 + 324 + 100 + 4 + 81}{6} \approx 147.67\]
Take the Square Root of the Average of the Squared Differences: This is our final step, and it produces our standard deviation.

Why? Since we squared the differences in step 3, we have square units. Taking the square root brings this value back to its original unit, giving us a measure of data spread that we can directly compare with the values in our data.

Let’s calculate the square root:

\[\sigma = \sqrt{\frac{\sum{(X - \mu)^2}}{N}} = \sqrt{147.67} \approx 12.15\]

So, the standard deviation of our dataset [46, 69, 32, 60, 52, 41] is approximately 12.15.

We’ll cover more about this in the next session on Distribution Statistics.

Standard deviation calculator

You can calculate the standard deviation by hand or with the help of our standard deviation calculator below.

# @title #### Standard deviation calculator
import gradio as gr
import numpy as np

def calculate_std_dev(numbers):
    numbers = [float(num) for num in numbers.split(',')]
    pop_std_dev = np.std(numbers)  # population standard deviation
    sample_std_dev = np.std(numbers, ddof=1)  # sample standard deviation
    return pop_std_dev, sample_std_dev

iface = gr.Interface(fn=calculate_std_dev, 
                     inputs="text", 
                     outputs=[
                         gr.Label(label="Population Standard Deviation"),
                         gr.Label(label="Sample Standard Deviation")
                     ],
                     examples=[['21,50,62,85,90'], ['12,34,56'], ['11,22,33,44,55']])
iface.launch()

The empirical rule

The empirical rule, or the 68-95-99.7 rule, tells you where your values lie: - About 68% of your values will fall within 1 standard deviation. - About 95% of your values will fall within 2 standard deviation. - About 99.7% of your values will fall within 3 standard deviation.

This is very useful in forecasting the final outcome. It gives a rough estimate of how certain an outcome will/will not happen.

For Example, the average height of an adult male in Indonesia is 5’10” with a standard deviation of 3 inches. Using empirical rule, it means that:

68% of Indonesian men are 5’10” plus or minus 3 inches tall
95% of Indonesian men are 5’10” plus or minus 6 inches tall,
99.7% of Indonesian men have a height of 5’10” plus or minus 9 inches.

Therefore, only about 0.3% of Indonesian men deviate more than 9 inches from the average, with 0.15% taller than 6’7”, and 0.15% shorter than 5’1”.

Using the height example, we can safely say that it’s very unlikely that we will meet Indonesian men who are taller than 6’7”.

Role of Standard Deviation in Machine Learning

In the realm of machine learning, understanding the standard deviation is key as it provides insights into the variability of data. Many algorithms require data to be normalized, and knowledge of data variability helps improve a model’s accuracy, thus enabling more reliable predictions. 🎯

Explore standard deviation here: geogebra.org

Interactive chart mode

You can explore various different data to get the variance, standard deviation value and learn how the value is positioned from our tool below.

# @title #### Bar chart, plot histogram and bellcurve
import warnings
warnings.filterwarnings('ignore', category=UserWarning, module='gradio')
import matplotlib.pyplot as plt
from scipy.stats import norm
import plotly.graph_objects as go
import gradio as gr
import plotly.io as pio
from PIL import Image
import io
import numpy as np
    
# Function to calculate mean, variance, standard deviation and plot bar chart
def interactive_bar(num_scores, scores, statistics_to_show=None, sort_data=False):
    scores_names = ['score1', 'score2', 'score3', 'score4', 'score5', 'score6'][:num_scores]

    # Sort the data if the option is selected
    if sort_data:
        scores, scores_names = zip(*sorted(zip(scores, scores_names), key=lambda pair: pair[0]))
    
    fig = go.Figure(data=go.Bar(y=scores, x=scores_names, name='scores'))

    # Calculate the mean
    mean_score = np.mean(scores)

    # Add a horizontal line for the mean
    fig.add_trace(go.Scatter(x=[scores_names[0], scores_names[-1]], y=[mean_score, mean_score], mode='lines', name=f'Mean: {mean_score:.2f}', line=dict(color='Red', width=1, dash='dash')))

    if 'variance' in statistics_to_show:
        # Calculate the variance
        variance = np.var(scores)

        # Add a text annotation for the variance
        fig.add_annotation(text=f'Variance: {variance:.2f}',
                           xref='paper', x=0.95, yref='paper', y=0.95,
                           showarrow=False, font=dict(size=14), bgcolor='white')

    if 'std_dev' in statistics_to_show:
        # Calculate the standard deviation
        std_dev = np.std(scores, ddof=1)

        # Add a text annotation for the standard deviation
        fig.add_annotation(text=f'Standard Deviation: {std_dev:.2f}',
                           xref='paper', x=0.95, yref='paper', y=0.9,
                           showarrow=False, font=dict(size=14), bgcolor='white')

    # Add labels for x and y axis
    fig.update_layout(
        xaxis_title="scores",
        yaxis_title="Value",
        font=dict(size=14),
    )

    # Convert the figure to PNG image
    png_image = pio.to_image(fig, format='png')

    # Create a PIL Image object for Gradio Output
    image = Image.open(io.BytesIO(png_image))

    return image

# Function to create a bell curve
def bell_curve(mean, std_dev):
    x = np.linspace(mean - 3.5*std_dev, mean + 3.5*std_dev, 100)
    plt.plot(x, norm.pdf(x, mean, std_dev), label=f"mean = {mean:.2f}, std_dev = {std_dev:.2f}")
    
    # Highlight areas within 1, 2, and 3 standard deviations of the mean
    plt.fill_between(x, norm.pdf(x, mean, std_dev), where=((x < mean + std_dev) & (x > mean - std_dev)), alpha=0.6, color='grey')
    plt.fill_between(x, norm.pdf(x, mean, std_dev), where=((x < mean + 2*std_dev) & (x > mean - 2*std_dev)), alpha=0.4, color='grey')
    plt.fill_between(x, norm.pdf(x, mean, std_dev), where=((x < mean + 3*std_dev) & (x > mean - 3*std_dev)), alpha=0.2, color='grey')

    # Add vertical lines for the mean and standard deviation
    plt.axvline(mean, color='red', linestyle='-', linewidth=2, label=f'Mean: {mean:.2f}')
    plt.axvline(mean-std_dev, color='blue', linestyle='--', linewidth=2, label=f'1 Std Dev below: {mean-std_dev:.2f}')
    plt.axvline(mean+std_dev, color='blue', linestyle='--', linewidth=2, label=f'1 Std Dev above: {mean+std_dev:.2f}')

    # Place the legend outside of the plot
    plt.legend(loc='upper left', bbox_to_anchor=(1,1))

    # Add labels for the mean and standard deviation multiples
    plt.text(mean, 0.01, 'Average', horizontalalignment='center', fontsize=13)
    plt.text(mean-std_dev, 0.01, '1 below', horizontalalignment='center', fontsize=10)
    plt.text(mean+std_dev, 0.01, '1 above', horizontalalignment='center', fontsize=10)
    plt.text(mean-2*std_dev, 0.01, '2 below', horizontalalignment='center', fontsize=10)
    plt.text(mean+2*std_dev, 0.01, '2 above', horizontalalignment='center', fontsize=10)
    plt.text(mean-3*std_dev, 0.01, '3 below', horizontalalignment='center', fontsize=10)
    plt.text(mean+3*std_dev, 0.01, '3 above', horizontalalignment='center', fontsize=10)

    plt.title("Distribution of Test Scores")
    plt.xlabel("Test Scores")
    plt.ylabel("Number of Students")

    # Convert the Matplotlib figure to a PIL Image and return it
    buf = io.BytesIO()
    plt.savefig(buf, format='png', bbox_inches='tight')
    buf.seek(0)
    image = Image.open(buf)

    return image

# Final function for Gradio interface
def final_fn(num_scores, score1=0, score2=0, score3=0, score4=0, score5=0, score6=0, statistics_to_show=None, sort_data=False):
    num_scores = int(num_scores)  # Convert num_scores to integer
    scores = [score1, score2, score3, score4, score5, score6][:num_scores]

    mean = np.mean(scores)
    std_dev = np.std(scores, ddof=1)

    bar_image = interactive_bar(num_scores, scores, statistics_to_show, sort_data)
    bell_image = bell_curve(mean, std_dev)

    return bar_image, bell_image


# Create Gradio interface
iface = gr.Interface(
    title="Standard Deviation and Variance",
    live=True,
    fn=final_fn,
    inputs=[
        gr.Dropdown(choices=[1, 2, 3, 4, 5, 6], label="Number of scores to use", value="6"),
        gr.Slider(minimum=0, maximum=100, step=1, value=46),
        gr.Slider(minimum=0, maximum=100, step=1, value=69),
        gr.Slider(minimum=0, maximum=100, step=1, value=32),
        gr.Slider(minimum=0, maximum=100, step=1, value=60),
        gr.Slider(minimum=0, maximum=100, step=1, value=52),
        gr.Slider(minimum=0, maximum=100, step=1, value=41),
        gr.CheckboxGroup(choices=['variance', 'std_dev'], value=['variance', 'std_dev'], label="Statistics to show"),
        gr.Checkbox(label="Sort data")
    ], 
    outputs=[gr.Image(type='pil', label='Bar Chart'), gr.Image(type='pil', label='Bell Curve')],
)

iface.launch()