Today we will learn about calculus, which is the study of change. Calculus is a branch of mathematics that is used to study continuous change. It has two main branches: differential calculus and integral calculus. Differential calculus is used to study the rate of change of a function, while integral calculus is used to study the accumulation of quantities, or the area under a curve.
We all - probably know - that the derivative of
\[ f(x) = 2x^3 + 3x^2 + 2x + 5 \]
is \[ f'(x) = 6x^2 + 6x + 2 \]
But what does that mean?
The derivative of a function \(f(x)\) is actually defined as:
\[ \frac{df(x)}{dx} = \lim_{\delta \to 0} \frac{f(x+\delta) - f(x)}{\delta} \]
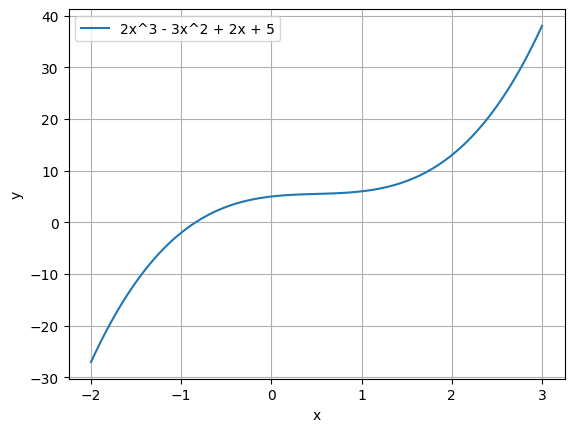
To understand what this means, let’s plot \(f(x)\) and \(f'(x)\).
# Plot 2x^3 - 3x^2 + 2x + 5
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 3, 100)
y = 2*x**3 - 3*x**2 + 2*x + 5
plt.plot(x, y)
plt.xlabel('x')
plt.ylabel('y')
# add legend
plt.legend(['2x^3 - 3x^2 + 2x + 5'])
plt.grid()
plt.show()
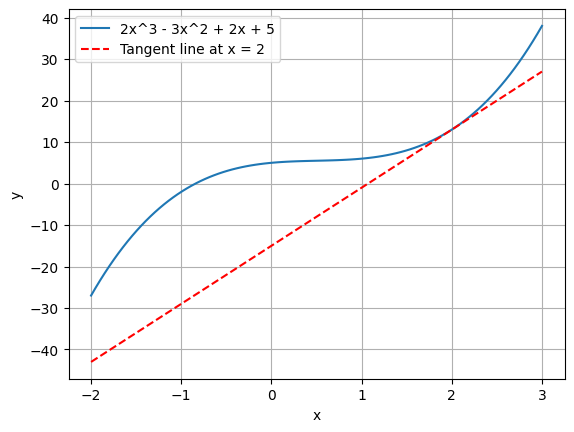
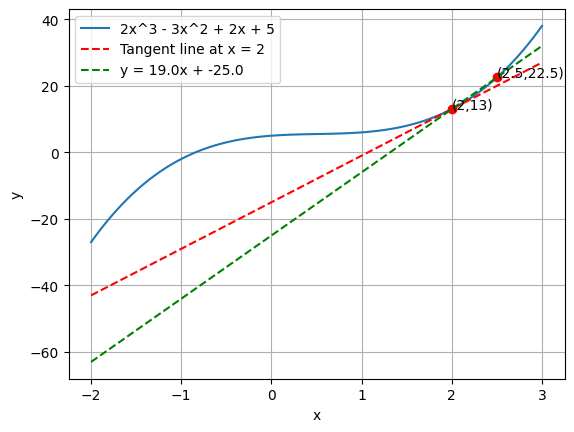
Now, let’s plot a tangent line to \(f(x)\) at \(x=2\).
# Plot 2x^3 - 3x^2 + 2x + 5
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 3, 100)
y = 2*x**3 - 3*x**2 + 2*x + 5
# Tangent line at x = 2
x1 = 2
y1 = 2*x1**3 - 3*x1**2 + 2*x1 + 5
m = 6*x1**2 - 6*x1 + 2
y2 = m*(x - x1) + y1
# Plot the main function
plt.plot(x, y)
# Plot tangent line
plt.plot(x, y2, 'r--')
plt.legend(['2x^3 - 3x^2 + 2x + 5', 'Tangent line at x = 2'])
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.show()
What is the slope of the tangent line at \(x=2\)?
That’s right, it’s \(f'(2)\).
But - without the knowledge of calculus - how would we calculate that slope?
Actually we can, we just need to zoom in and calculate the slope of the line that is “close enough” to the tangent line.
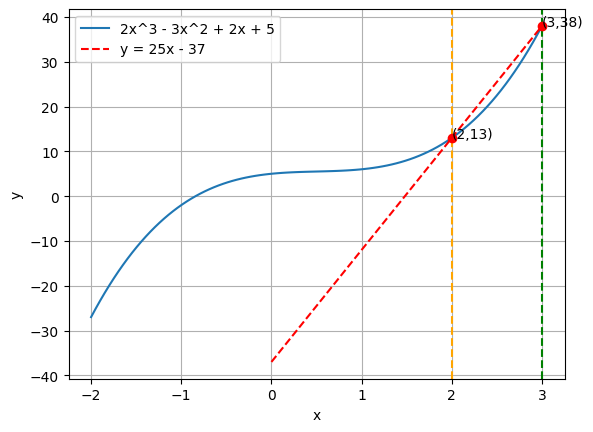
# Plot 2x^3 - 3x^2 + 2x + 5
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return 2*x**3 - 3*x**2 + 2*x + 5
x = np.linspace(-2, 3, 100)
y = f(x)
# Plot the main function
plt.plot(x, y)
# Create a vertical line at x = 2 and x = 3
plt.axvline(x=2, color='orange', linestyle='--')
plt.axvline(x=3, color='g', linestyle='--')
plt.legend(['2x^3 - 3x^2 + 2x + 5'])
x1 = 2
y1 = f(x1)
# create a dot at (x1, y1) with label (2, y1)
plt.plot(x1, y1, 'ro')
plt.annotate('({},{})'.format(x1, y1), xy=(x1, y1), xytext=(x1, y1))
x2 = 3
y2 = f(x2)
# create a dot at (x2, y2) with label (3, y2)
plt.plot(x2, y2, 'ro')
plt.annotate('({},{})'.format(x2, y2), xy=(x2, y2), xytext=(x2, y2))
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.show()
Then create a straight line from \(x=2\) to \(x=3\).
The slope of that line is:
\[ m = \frac{f(3) - f(2)}{3 - 2} = \frac{38-13}{3-2} = 25 \]
The y-intercept of that line is:
\[ f(x) = mx + c\\ c = f(x) - mx \]
Substitute \(x=2\) and \(y=f(2)\): \[ c = f(2) - m \cdot 2 = 13 - 25 \cdot 2 = -37 \]
So the equation of the line is: \[ y = 25x - 37 \]
Let’s draw that line.
# Plot 2x^3 - 3x^2 + 2x + 5
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return 2*x**3 - 3*x**2 + 2*x + 5
x = np.linspace(-2, 3, 100)
y = f(x)
# Plot the main function
plt.plot(x, y, label='2x^3 - 3x^2 + 2x + 5')
# Create a vertical line at x = 2 and x = 3
plt.axvline(x=2, color='orange', linestyle='--')
plt.axvline(x=3, color='g', linestyle='--')
x1 = 2
y1 = f(x1)
# create a dot at (x1, y1) with label (2, y1)
plt.plot(x1, y1, 'ro')
plt.annotate('({},{})'.format(x1, y1), xy=(x1, y1), xytext=(x1, y1))
x2 = 3
y2 = f(x2)
# create a dot at (x2, y2) with label (3, y2)
plt.plot(x2, y2, 'ro')
plt.annotate('({},{})'.format(x2, y2), xy=(x2, y2), xytext=(x2, y2))
# Draw y = 25x - 37
x3 = np.linspace(0, 3, 100)
y3 = 25*x3 - 37
plt.plot(x3, y3, 'r--', label='y = 25x - 37')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.show()
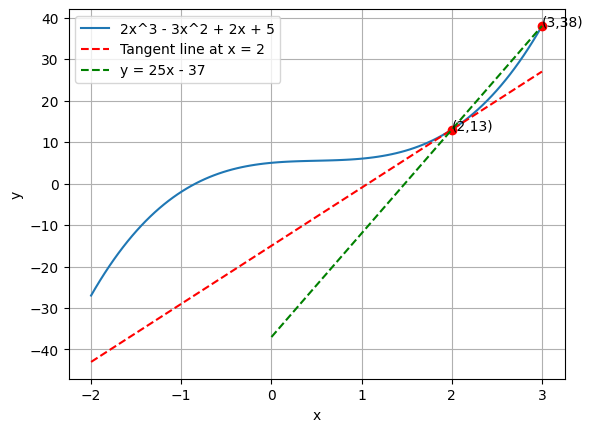
Now we know that the slop is \(37\), but that’s not the exact slope of the tangent line.
Let’s draw both lines together
# Plot 2x^3 - 3x^2 + 2x + 5
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 3, 100)
y = 2*x**3 - 3*x**2 + 2*x + 5
# Tangent line at x = 2
x1 = 2
y1 = 2*x1**3 - 3*x1**2 + 2*x1 + 5
m = 6*x1**2 - 6*x1 + 2
y2 = m*(x - x1) + y1
# Plot the main function
plt.plot(x, y, label="2x^3 - 3x^2 + 2x + 5")
# Plot tangent line
plt.plot(x, y2, 'r--', label='Tangent line at x = 2')
x1 = 2
y1 = f(x1)
# create a dot at (x1, y1) with label (2, y1)
plt.plot(x1, y1, 'ro')
plt.annotate('({},{})'.format(x1, y1), xy=(x1, y1), xytext=(x1, y1))
x2 = 3
y2 = f(x2)
# create a dot at (x2, y2) with label (3, y2)
plt.plot(x2, y2, 'ro')
plt.annotate('({},{})'.format(x2, y2), xy=(x2, y2), xytext=(x2, y2))
# Draw y = 25x - 37
x3 = np.linspace(0, 3, 100)
y3 = 25*x3 - 37
plt.plot(x3, y3, 'g--', label='y = 25x - 37')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.show()
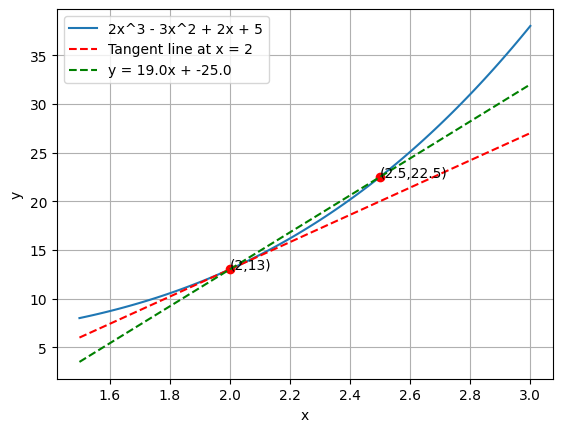
Hmm, not quite right. Perhaps, let’s try drawing line at x = 2$ and \(x = 2.5\)?
# Plot 2x^3 - 3x^2 + 2x + 5
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-2, 3, 100)
y = 2*x**3 - 3*x**2 + 2*x + 5
# Tangent line at x = 2
x1 = 2
y1 = 2*x1**3 - 3*x1**2 + 2*x1 + 5
m = 6*x1**2 - 6*x1 + 2
y2 = m*(x - x1) + y1
# Plot the main function
plt.plot(x, y, label="2x^3 - 3x^2 + 2x + 5")
# Plot tangent line
plt.plot(x, y2, 'r--', label='Tangent line at x = 2')
x1 = 2
y1 = f(x1)
# create a dot at (x1, y1) with label (2, y1)
plt.plot(x1, y1, 'ro')
plt.annotate('({},{})'.format(x1, y1), xy=(x1, y1), xytext=(x1, y1))
x2 = 2.5
y2 = f(x2)
# create a dot at (x2, y2) with label (3, y2)
plt.plot(x2, y2, 'ro')
plt.annotate('({},{})'.format(x2, y2), xy=(x2, y2), xytext=(x2, y2))
m = (y2 - y1) / (x2 - x1)
c = y2 - m*x2
y3 = m*x + c
plt.plot(x, y3, 'g--', label='y = {}x + {}'.format(m, c))
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.show()
It’s getting closer to the tangent line. Let’s zoom in the graph
# Plot 2x^3 - 3x^2 + 2x + 5
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(1.5, 3, 100)
y = 2*x**3 - 3*x**2 + 2*x + 5
# Tangent line at x = 2
x1 = 2
y1 = 2*x1**3 - 3*x1**2 + 2*x1 + 5
m = 6*x1**2 - 6*x1 + 2
y2 = m*(x - x1) + y1
# Plot the main function
plt.plot(x, y, label="2x^3 - 3x^2 + 2x + 5")
# Plot tangent line
plt.plot(x, y2, 'r--', label='Tangent line at x = 2')
x1 = 2
y1 = f(x1)
# create a dot at (x1, y1) with label (2, y1)
plt.plot(x1, y1, 'ro')
plt.annotate('({},{})'.format(x1, y1), xy=(x1, y1), xytext=(x1, y1))
x2 = 2.5
y2 = f(x2)
# create a dot at (x2, y2) with label (3, y2)
plt.plot(x2, y2, 'ro')
plt.annotate('({},{})'.format(x2, y2), xy=(x2, y2), xytext=(x2, y2))
m = (y2 - y1) / (x2 - x1)
c = y2 - m*x2
y3 = m*x + c
plt.plot(x, y3, 'g--', label='y = {}x + {}'.format(m, c))
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.show()
The idea is, if we can get \(x_2\) closer to \(x_1\), we can get the slope of the line closer to the tangent line.
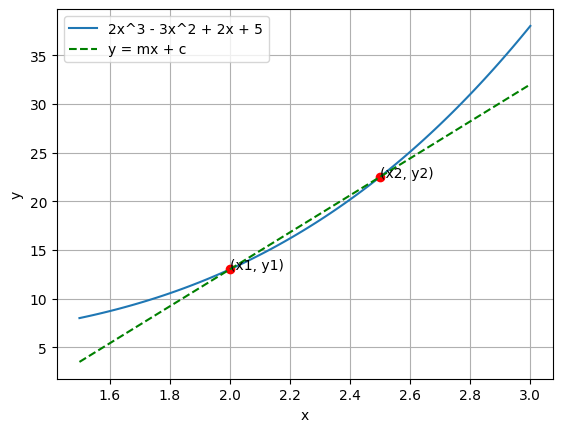
Let’s try to generalize
# Plot 2x^3 - 3x^2 + 2x + 5
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(1.5, 3, 100)
y = 2*x**3 - 3*x**2 + 2*x + 5
# Plot the main function
plt.plot(x, y, label="2x^3 - 3x^2 + 2x + 5")
x1 = 2
y1 = f(x1)
# create a dot at (x1, y1) with label (2, y1)
plt.plot(x1, y1, 'ro')
plt.annotate('(x1, y1)', xy=(x1, y1), xytext=(x1, y1))
x2 = 2.5
y2 = f(x2)
# create a dot at (x2, y2) with label (3, y2)
plt.plot(x2, y2, 'ro')
plt.annotate('(x2, y2)', xy=(x2, y2), xytext=(x2, y2))
m = (y2 - y1) / (x2 - x1)
c = y2 - m*x2
y3 = m*x + c
plt.plot(x, y3, 'g--', label='y = mx + c')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.show()
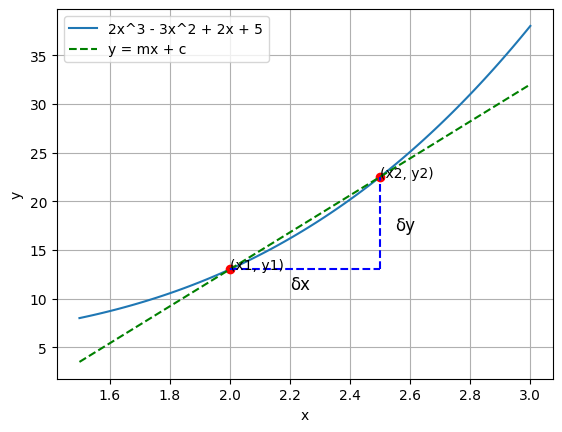
To find the slope, we need to find the change in \(y\) divided by the change in \(x\).
# Plot 2x^3 - 3x^2 + 2x + 5
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(1.5, 3, 100)
y = 2*x**3 - 3*x**2 + 2*x + 5
# Plot the main function
plt.plot(x, y, label="2x^3 - 3x^2 + 2x + 5")
x1 = 2
y1 = f(x1)
# create a dot at (x1, y1) with label (2, y1)
plt.plot(x1, y1, 'ro')
plt.annotate('(x1, y1)', xy=(x1, y1), xytext=(x1, y1))
x2 = 2.5
y2 = f(x2)
# create a dot at (x2, y2) with label (3, y2)
plt.plot(x2, y2, 'ro')
plt.annotate('(x2, y2)', xy=(x2, y2), xytext=(x2, y2))
m = (y2 - y1) / (x2 - x1)
c = y2 - m*x2
y3 = m*x + c
plt.plot(x, y3, 'g--', label='y = mx + c')
x4 = np.linspace(x1, x2, 100)
y4 = np.linspace(y1, y1, 100)
plt.plot(x4, y4, 'b--')
# add text near that plot
plt.text(2.2, 11, 'δx', fontsize=12)
x5 = np.linspace(x2, x2, 100)
y5 = np.linspace(y1, y2, 100)
plt.plot(x5, y5, 'b--')
# add text near that plot
plt.text(2.55, 17, 'δy', fontsize=12)
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.show()
The slope \(m\) is:
\[ m = \frac{f(x_2) - f(x_1)}{x_2 - x_1} \]
\[ m = \frac{f(x_1 + \delta x) - f(x_1)}{\delta x} \]
Since \(m\) is \(\frac{\delta y}{\delta x}\)
\[ \frac{\delta y}{\delta x} = \frac{f(x_1 + \delta x) - f(x_1)}{\delta x} \]
If we let \(\delta x\) approach \(0\), we get the tangent line:
\[ \frac{df(x)}{dx} = \lim_{\delta x \to 0} \frac{f(x_1 + \delta x) - f(x_1)}{\delta x} \]
Interestingly, we can derive many different derivative formula using this method.
For example, the derivative of \(f(x) = x^2\) is:
\[ \frac{df(x)}{dx} = \lim_{\delta x \to 0} \frac{(x + \delta x)^2 - x^2}{\delta x} = \lim_{\delta x \to 0} \frac{x^2 + 2x\delta x + \delta x^2 - x^2}{\delta x} = \lim_{\delta x \to 0} \frac{2x\delta x + \delta x^2}{\delta x} = \lim_{\delta x \to 0} 2x + \delta x \]
Since \(\delta x\) approaches \(0\), we can ignore it:
\[ \frac{df(x)}{dx} = 2x \]
One more example, the derivative of \(f(x) = x^3\) is:
\[ \frac{df(x)}{dx} = \lim_{\delta x \to 0} \frac{(x + \delta x)^3 - x^3}{\delta x} = \lim_{\delta x \to 0} \frac{x^3 + 3x^2\delta x + 3x\delta x^2 + \delta x^3 - x^3}{\delta x} = \lim_{\delta x \to 0} \frac{3x^2\delta x + 3x\delta x^2 + \delta x^3}{\delta x} = \lim_{\delta x \to 0} 3x^2 + 3x\delta x + \delta x^2 \]
Since \(\delta x\) approaches \(0\), we can ignore it:
\[ \frac{df(x)}{dx} = 3x^2 \]
Here we only list down the rules, but actually the concepts are simple.
Please watch the following videos:
Visualizing the chain rule and product rule | Chapter 4, Essence of calculus
\[ \frac{d}{dx} (f(x) + g(x)) = \frac{df(x)}{dx} + \frac{dg(x)}{dx} \]
Example:
\[ \frac{d}{dx} (x^2 + 2x) = \frac{d}{dx} (x^2) + \frac{d}{dx} (2x) = 2x + 2 \]
\[ \frac{d}{dx} (f(x) \cdot g(x)) = f(x) \cdot \frac{dg(x)}{dx} + g(x) \cdot \frac{df(x)}{dx} \]
Example:
\[ \frac{d}{dx} (x^2 \cdot 2x) = x^2 \cdot \frac{d}{dx} (2x) + 2x \cdot \frac{d}{dx} (x^2) = x^2 \cdot 2 + 2x \cdot 2x = 6x^2 \]
\[ \frac{d}{dx} (x^n) = n \cdot x^{n-1} \]
Example:
\[ \frac{d}{dx} (x^3) = 3x^2 \]
\[ \frac{d}{dx} f(g(x)) = \frac{df(g(x))}{dg(x)} \cdot \frac{dg(x)}{dx} \]
Or it can also be written as:
Let’s denote \(u = g(x)\):
\[ \frac{d}{dx} f(u) = \frac{df(u)}{du} \cdot \frac{du}{dx} \]
Please remember this rule, it will be used a lot in deep learning.