import torch
class Net(torch.nn.Module):
def __init__(self, n_feature, n_hidden, n_output):
super().__init__()
self.layer_1 = torch.nn.Linear(n_feature, n_hidden)
self.layer_2 = torch.nn.Linear(n_hidden, n_output)
def forward(self, x):
return self.layer_2(torch.relu(self.layer_1(x)))Pytorch Application
Simple Line Fitting
Let’s define a simple Neural Network with one hidden layer and one output layer.
Tips: to generate numbers from -1 to 1 we can use linspace:
import torch
x = torch.linspace(-1, 1, 100)
print(x)
print(x.shape)tensor([-1.0000, -0.9798, -0.9596, -0.9394, -0.9192, -0.8990, -0.8788, -0.8586,
-0.8384, -0.8182, -0.7980, -0.7778, -0.7576, -0.7374, -0.7172, -0.6970,
-0.6768, -0.6566, -0.6364, -0.6162, -0.5960, -0.5758, -0.5556, -0.5354,
-0.5152, -0.4949, -0.4747, -0.4545, -0.4343, -0.4141, -0.3939, -0.3737,
-0.3535, -0.3333, -0.3131, -0.2929, -0.2727, -0.2525, -0.2323, -0.2121,
-0.1919, -0.1717, -0.1515, -0.1313, -0.1111, -0.0909, -0.0707, -0.0505,
-0.0303, -0.0101, 0.0101, 0.0303, 0.0505, 0.0707, 0.0909, 0.1111,
0.1313, 0.1515, 0.1717, 0.1919, 0.2121, 0.2323, 0.2525, 0.2727,
0.2929, 0.3131, 0.3333, 0.3535, 0.3737, 0.3939, 0.4141, 0.4343,
0.4545, 0.4747, 0.4949, 0.5152, 0.5354, 0.5556, 0.5758, 0.5960,
0.6162, 0.6364, 0.6566, 0.6768, 0.6970, 0.7172, 0.7374, 0.7576,
0.7778, 0.7980, 0.8182, 0.8384, 0.8586, 0.8788, 0.8990, 0.9192,
0.9394, 0.9596, 0.9798, 1.0000])
torch.Size([100])However, what we want is (100, 1) shape. Why? Because we want to model 100 samples with 1 feature each.
So, we need to unsqueeze it
import torch
x = torch.unsqueeze(torch.linspace(-1, 1, 100), 1)
print(x)
print(x.shape)tensor([[-1.0000],
[-0.9798],
[-0.9596],
[-0.9394],
[-0.9192],
[-0.8990],
[-0.8788],
[-0.8586],
[-0.8384],
[-0.8182],
[-0.7980],
[-0.7778],
[-0.7576],
[-0.7374],
[-0.7172],
[-0.6970],
[-0.6768],
[-0.6566],
[-0.6364],
[-0.6162],
[-0.5960],
[-0.5758],
[-0.5556],
[-0.5354],
[-0.5152],
[-0.4949],
[-0.4747],
[-0.4545],
[-0.4343],
[-0.4141],
[-0.3939],
[-0.3737],
[-0.3535],
[-0.3333],
[-0.3131],
[-0.2929],
[-0.2727],
[-0.2525],
[-0.2323],
[-0.2121],
[-0.1919],
[-0.1717],
[-0.1515],
[-0.1313],
[-0.1111],
[-0.0909],
[-0.0707],
[-0.0505],
[-0.0303],
[-0.0101],
[ 0.0101],
[ 0.0303],
[ 0.0505],
[ 0.0707],
[ 0.0909],
[ 0.1111],
[ 0.1313],
[ 0.1515],
[ 0.1717],
[ 0.1919],
[ 0.2121],
[ 0.2323],
[ 0.2525],
[ 0.2727],
[ 0.2929],
[ 0.3131],
[ 0.3333],
[ 0.3535],
[ 0.3737],
[ 0.3939],
[ 0.4141],
[ 0.4343],
[ 0.4545],
[ 0.4747],
[ 0.4949],
[ 0.5152],
[ 0.5354],
[ 0.5556],
[ 0.5758],
[ 0.5960],
[ 0.6162],
[ 0.6364],
[ 0.6566],
[ 0.6768],
[ 0.6970],
[ 0.7172],
[ 0.7374],
[ 0.7576],
[ 0.7778],
[ 0.7980],
[ 0.8182],
[ 0.8384],
[ 0.8586],
[ 0.8788],
[ 0.8990],
[ 0.9192],
[ 0.9394],
[ 0.9596],
[ 0.9798],
[ 1.0000]])
torch.Size([100, 1])Let’s put them all together:
import torch
import numpy as np
import matplotlib.pyplot as plt
torch.manual_seed(1) # make it reproducible
# 1. Generate data
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1)
# x^2 + 0.2*noise
y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1)
# 2. Build the network
net = Net(n_feature=1, n_hidden=10, n_output=1)
print(net)
# 3. Train the network
optimizer = torch.optim.SGD(net.parameters(), lr=0.2)
# Mean square error
loss_func = torch.nn.MSELoss()
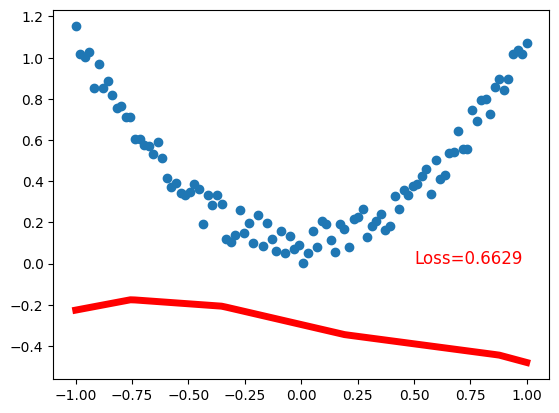
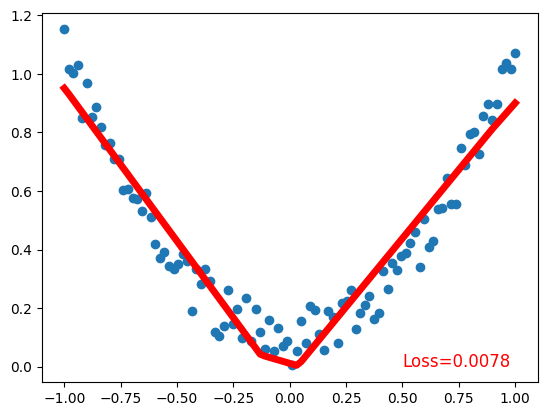
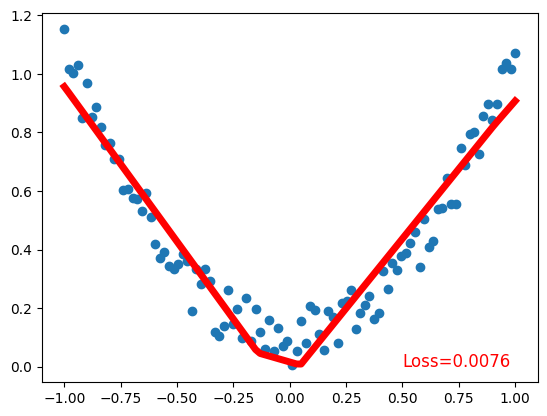
for t in range(200):
prediction = net(x)
loss = loss_func(prediction, y)
optimizer.zero_grad() # clear gradients for next train
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if t % 20 == 0:
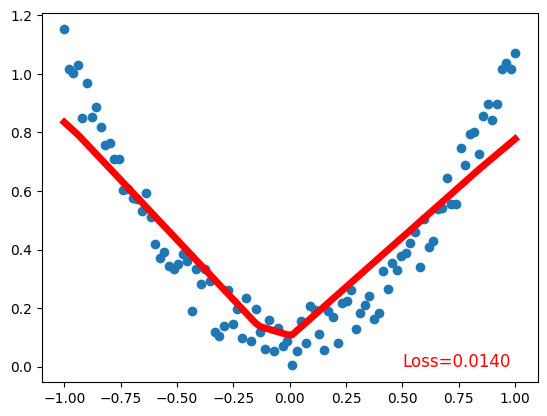
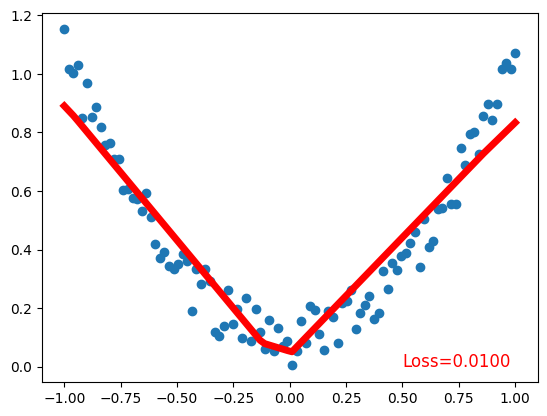
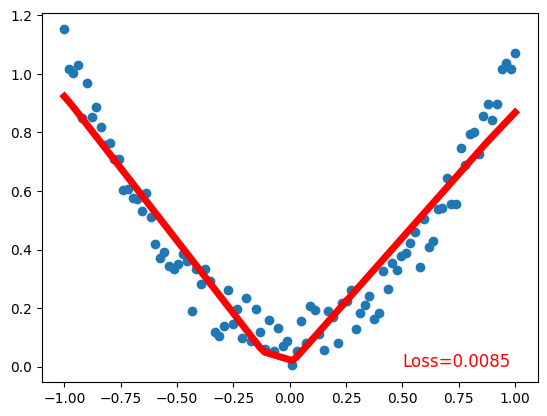
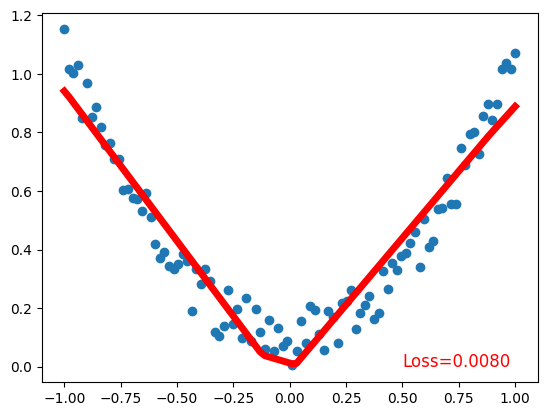
plt.scatter(x.data.numpy(), y.data.numpy()) # plot data
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5) # plot prediction
plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 12, 'color': 'red'}) # plot loss
plt.show()Net(
(layer_1): Linear(in_features=1, out_features=10, bias=True)
(layer_2): Linear(in_features=10, out_features=1, bias=True)
)
Validating the Model
Is it good enough? Does it overfit?
Let’s split the data into training and test sets.
## Draw quadratic equations
import torch
import numpy as np
import matplotlib.pyplot as plt
# Set random seed
torch.manual_seed(1) # reproducible
# 1. Generate data
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1)
# Split data into training and testing randomly
indices = torch.randperm(x.size(0))
x_train = torch.index_select(x, dim=0, index=indices[:80])
y_train = torch.index_select(y, dim=0, index=indices[:80])
x_test = torch.index_select(x, dim=0, index=indices[80:])
y_test = torch.index_select(y, dim=0, index=indices[80:])
# 2. Build the network
net = Net(n_feature=1, n_hidden=10, n_output=1) # define the network
print(net) # net architecture
# 3. Train the network
optimizer = torch.optim.SGD(net.parameters(), lr=0.2) # define optimizer
loss_func = torch.nn.MSELoss() # define loss function
for t in range(200):
net.train()
prediction = net(x_train) # input x and predict based on x
loss = loss_func(prediction, y_train) # must be (1. nn output, 2. target)
optimizer.zero_grad() # clear gradients for next train
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if t % 20 == 0:
# plot and show learning process
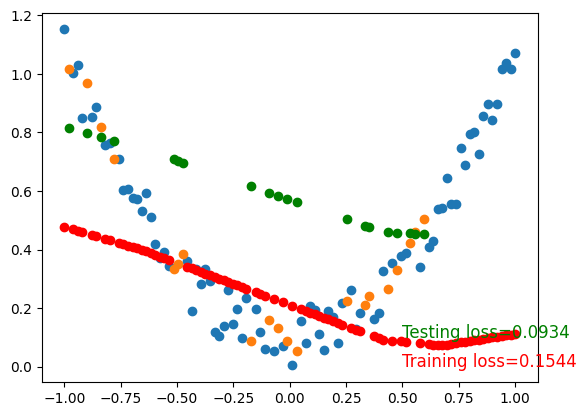
plt.scatter(x_train.data.numpy(), y_train.data.numpy()) # plot training data
plt.scatter(x_test.data.numpy(), y_test.data.numpy()) # plot testing data
# plot prediction scatter
plt.scatter(x_train.data.numpy(), prediction.data.numpy(), color='red')
net.eval()
# get prediction on test data
with torch.inference_mode():
test_prediction = net(x_test)
# plot prediction scatter
plt.scatter(x_test.data.numpy(), test_prediction.data.numpy(), color='green')
plt.text(0.5, 0, 'Training loss=%.4f' % loss.data.numpy(), fontdict={'size': 12, 'color': 'red'}) # plot loss
plt.text(0.5, 0.1, 'Testing loss=%.4f' % loss_func(test_prediction, y_test).data.numpy(), fontdict={'size': 12, 'color': 'green'})
plt.show()Net(
(layer_1): Linear(in_features=1, out_features=10, bias=True)
(layer_2): Linear(in_features=10, out_features=1, bias=True)
)
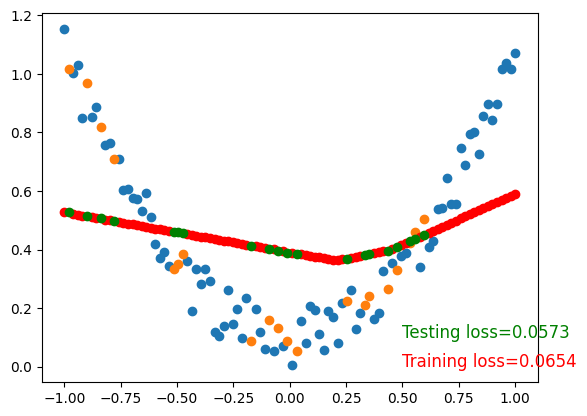
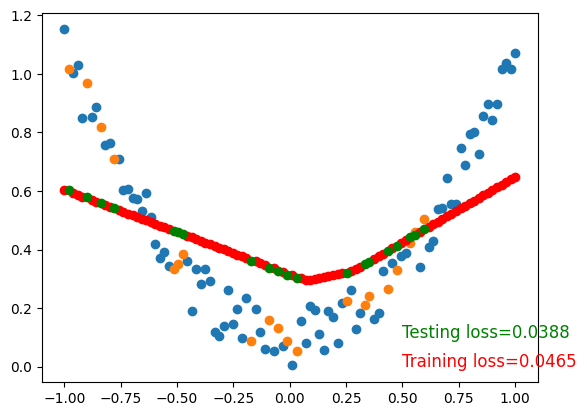
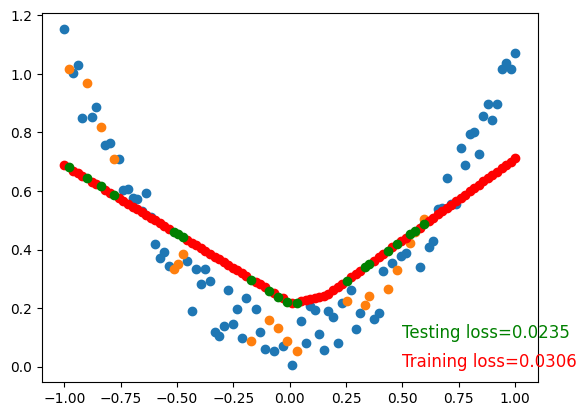
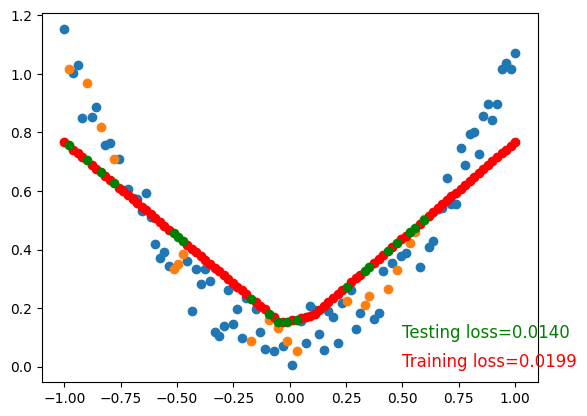
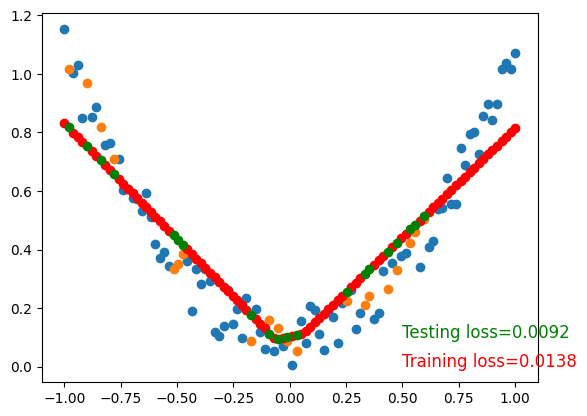
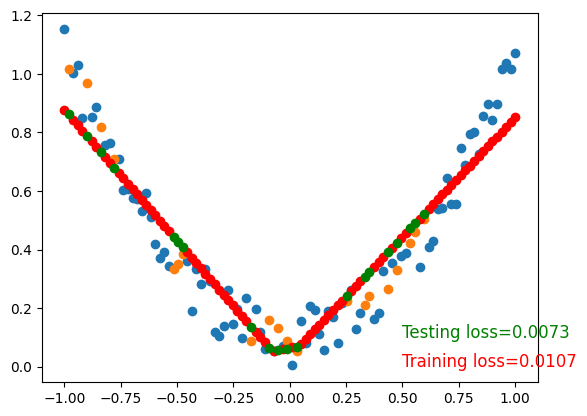
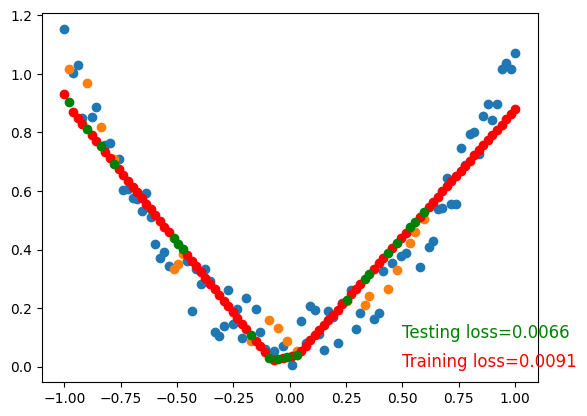
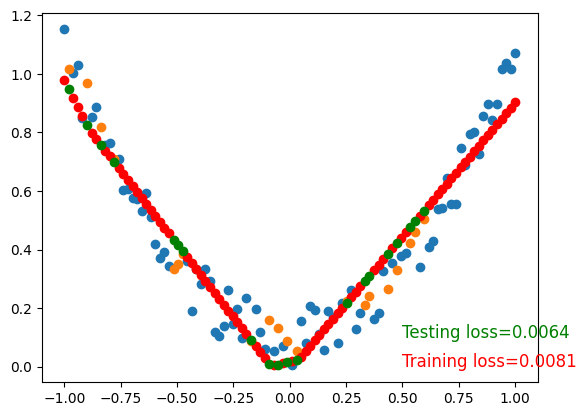
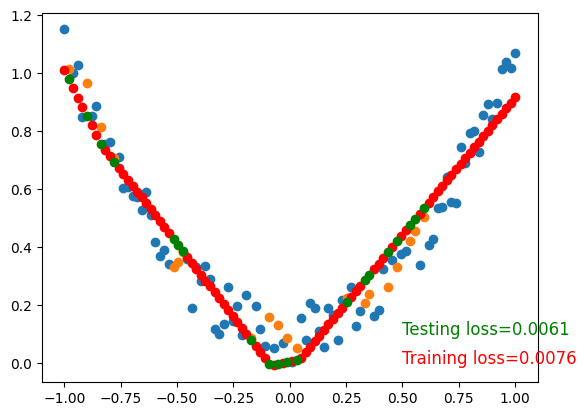
To visualize testing loss and training loss, we usually plot them together.
## Draw quadratic equations
import torch
import numpy as np
import matplotlib.pyplot as plt
# Set random seed
torch.manual_seed(1) # reproducible
# 1. Generate data
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1)
# Split data into training and testing randomly
indices = torch.randperm(x.size(0))
x_train = torch.index_select(x, dim=0, index=indices[:80])
y_train = torch.index_select(y, dim=0, index=indices[:80])
x_test = torch.index_select(x, dim=0, index=indices[80:])
y_test = torch.index_select(y, dim=0, index=indices[80:])
# 2. Build the network
net = Net(n_feature=1, n_hidden=10, n_output=1) # define the network
print(net) # net architecture
# 3. Train the network
optimizer = torch.optim.SGD(net.parameters(), lr=0.2) # define optimizer
loss_func = torch.nn.MSELoss() # define loss function
training_losses = []
testing_losses = []
for t in range(200):
net.train()
prediction = net(x_train) # input x and predict based on x
loss = loss_func(prediction, y_train) # must be (1. nn output, 2. target)
optimizer.zero_grad() # clear gradients for next train
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if t % 20 == 0:
net.eval()
with torch.inference_mode():
test_prediction = net(x_test)
test_loss = loss_func(test_prediction, y_test)
print('Training loss=%.4f' % loss.data.numpy())
print('Testing loss=%.4f' % test_loss.data.numpy())
print()
training_losses.append(loss.data.numpy())
testing_losses.append(test_loss.data.numpy())
plt.plot(training_losses, label='Training loss')
plt.plot(testing_losses, label='Testing loss')
plt.legend()
plt.show()Net(
(layer_1): Linear(in_features=1, out_features=10, bias=True)
(layer_2): Linear(in_features=10, out_features=1, bias=True)
)
Training loss=0.1544
Testing loss=0.0934
Training loss=0.0654
Testing loss=0.0573
Training loss=0.0465
Testing loss=0.0388
Training loss=0.0306
Testing loss=0.0235
Training loss=0.0199
Testing loss=0.0140
Training loss=0.0138
Testing loss=0.0092
Training loss=0.0107
Testing loss=0.0073
Training loss=0.0091
Testing loss=0.0066
Training loss=0.0081
Testing loss=0.0064
Training loss=0.0076
Testing loss=0.0061
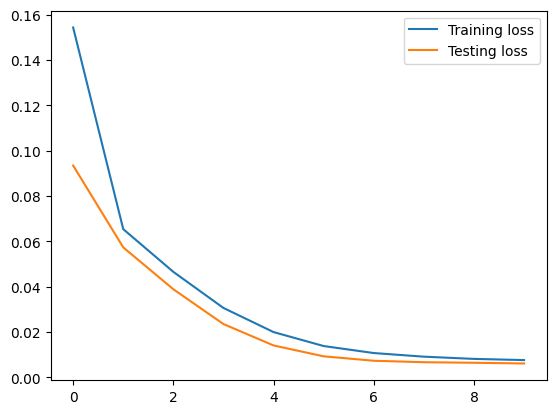
Overfitting
The indicator of overfitting is when the training loss is decreasing but the testing loss is increasing.
More Complex Model
# make moon from sklearn
import torch
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
# Set random seed
torch.manual_seed(1) # reproducible
# 1. Generate data
x, y = make_moons(n_samples=1000, noise=0.2, random_state=1)
x = torch.from_numpy(x).type(torch.FloatTensor)
y = torch.from_numpy(y).type(torch.LongTensor)
# Plot data
plt.scatter(x.numpy()[:, 0], x.numpy()[:, 1], c=y.numpy(), s=40, cmap=plt.cm.Spectral)
plt.show()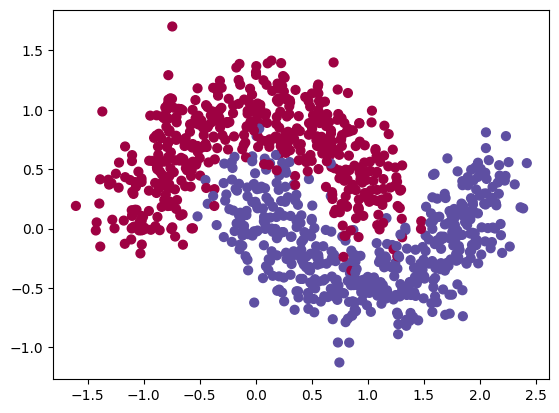
# make moon from sklearn
import torch
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
# Set random seed
torch.manual_seed(1) # reproducible
# 1. Generate data
x, y = make_moons(n_samples=1000, noise=0.2, random_state=1)
x = torch.from_numpy(x).type(torch.FloatTensor)
y = torch.from_numpy(y).type(torch.LongTensor)
# Split data into training and testing randomly
indices = torch.randperm(x.size(0))
x_train = torch.index_select(x, dim=0, index=indices[:800])
y_train = torch.index_select(y, dim=0, index=indices[:800])
x_test = torch.index_select(x, dim=0, index=indices[800:])
y_test = torch.index_select(y, dim=0, index=indices[800:])
# 2. Build the network
net = Net(n_feature=2, n_hidden=5, n_output=2) # define the network
# 3. Train the network
optimizer = torch.optim.SGD(net.parameters(), lr=0.2) # define optimizer
loss_func = torch.nn.CrossEntropyLoss() # define loss function
training_losses = []
testing_losses = []
for t in range(200):
net.train()
prediction = net(x_train) # input x and predict based on x
loss = loss_func(prediction, y_train) # must be (1. nn output, 2. target)
optimizer.zero_grad() # clear gradients for next train
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if t % 20 == 0:
net.eval()
with torch.inference_mode():
test_prediction = net(x_test)
test_loss = loss_func(test_prediction, y_test)
# print('Training loss=%.4f' % loss.data.numpy())
# print('Testing loss=%.4f' % test_loss.data.numpy())
# print()
training_losses.append(loss.data.numpy())
testing_losses.append(test_loss.data.numpy())
plt.plot(training_losses, label='Training loss')
plt.plot(testing_losses, label='Testing loss')
plt.legend()
plt.show()
plt.scatter(x.numpy()[:, 0], x.numpy()[:, 1], c=y.numpy(), s=40, cmap=plt.cm.Spectral)
# Draw model decision boundary
x_min, x_max = x[:, 0].min() - 0.5, x[:, 0].max() + 0.5
y_min, y_max = x[:, 1].min() - 0.5, x[:, 1].max() + 0.5
xx, yy = torch.meshgrid(torch.arange(x_min, x_max, 0.02), torch.arange(y_min, y_max, 0.02))
with torch.inference_mode():
Z = net(torch.cat((xx.reshape(-1, 1), yy.reshape(-1, 1)), dim=1))
Z = torch.argmax(Z, dim=1)
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.5)
plt.show()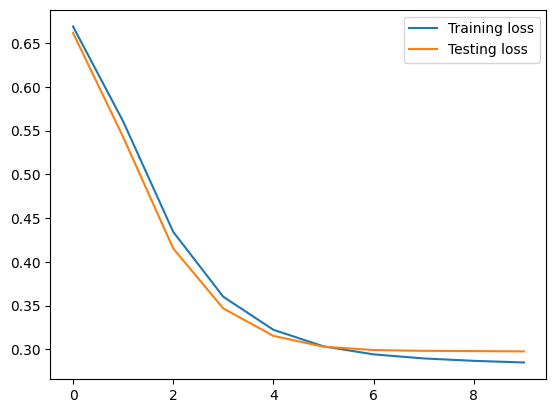
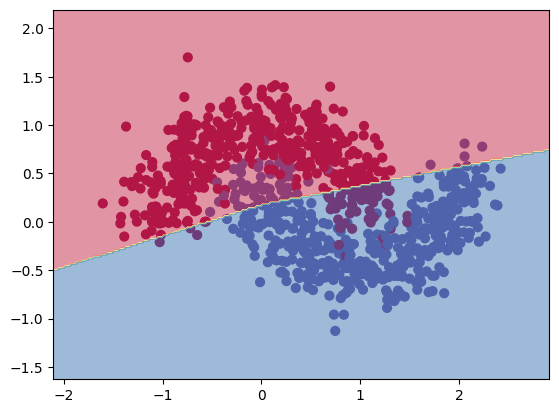
It seems the model overfits and the training loss is still high. Let’s try to increase the complexity of the model.
# make moon from sklearn
import torch
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
# Set random seed
torch.manual_seed(1) # reproducible
# 1. Generate data
x, y = make_moons(n_samples=1000, noise=0.2, random_state=1)
x = torch.from_numpy(x).type(torch.FloatTensor)
y = torch.from_numpy(y).type(torch.LongTensor)
# Split data into training and testing randomly
indices = torch.randperm(x.size(0))
x_train = torch.index_select(x, dim=0, index=indices[:800])
y_train = torch.index_select(y, dim=0, index=indices[:800])
x_test = torch.index_select(x, dim=0, index=indices[800:])
y_test = torch.index_select(y, dim=0, index=indices[800:])
# 2. Build the network
net = Net(n_feature=2, n_hidden=300, n_output=2) # define the network
# 3. Train the network
optimizer = torch.optim.SGD(net.parameters(), lr=0.2) # define optimizer
loss_func = torch.nn.CrossEntropyLoss() # define loss function
training_losses = []
testing_losses = []
for t in range(200):
net.train()
prediction = net(x_train) # input x and predict based on x
loss = loss_func(prediction, y_train) # must be (1. nn output, 2. target)
optimizer.zero_grad() # clear gradients for next train
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if t % 20 == 0:
net.eval()
with torch.inference_mode():
test_prediction = net(x_test)
test_loss = loss_func(test_prediction, y_test)
# print('Training loss=%.4f' % loss.data.numpy())
# print('Testing loss=%.4f' % test_loss.data.numpy())
# print()
training_losses.append(loss.data.numpy())
testing_losses.append(test_loss.data.numpy())
plt.plot(training_losses, label='Training loss')
plt.plot(testing_losses, label='Testing loss')
plt.legend()
plt.show()
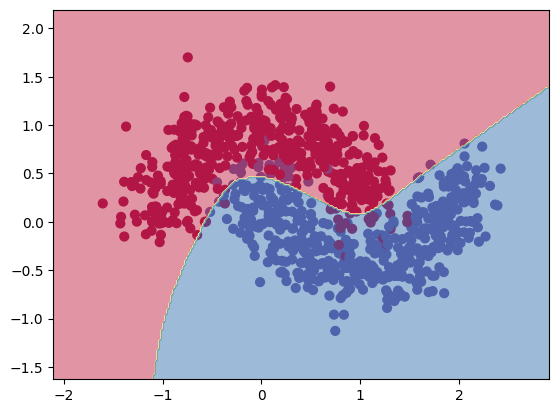
plt.scatter(x.numpy()[:, 0], x.numpy()[:, 1], c=y.numpy(), s=40, cmap=plt.cm.Spectral)
# Draw model decision boundary
x_min, x_max = x[:, 0].min() - 0.5, x[:, 0].max() + 0.5
y_min, y_max = x[:, 1].min() - 0.5, x[:, 1].max() + 0.5
xx, yy = torch.meshgrid(torch.arange(x_min, x_max, 0.02), torch.arange(y_min, y_max, 0.02))
with torch.inference_mode():
Z = net(torch.cat((xx.reshape(-1, 1), yy.reshape(-1, 1)), dim=1))
Z = torch.argmax(Z, dim=1)
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.5)
plt.show()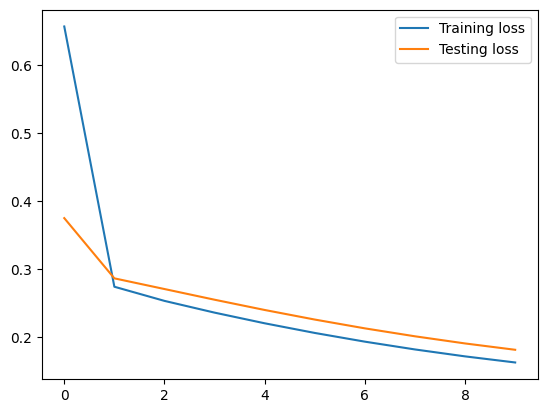
Pre-trained Model
Pytorch has a lot of pre-trained models. We can use them for transfer learning. We will learn more about transfer learning in the next session.
But let’s see one of them
from torchvision import models
resnet = models.resnet101(pretrained=True)/Users/ruangguru/.pyenv/versions/3.11.1/lib/python3.11/site-packages/torchvision/models/_utils.py:208: UserWarning: The parameter 'pretrained' is deprecated since 0.13 and may be removed in the future, please use 'weights' instead.
warnings.warn(
/Users/ruangguru/.pyenv/versions/3.11.1/lib/python3.11/site-packages/torchvision/models/_utils.py:223: UserWarning: Arguments other than a weight enum or `None` for 'weights' are deprecated since 0.13 and may be removed in the future. The current behavior is equivalent to passing `weights=ResNet101_Weights.IMAGENET1K_V1`. You can also use `weights=ResNet101_Weights.DEFAULT` to get the most up-to-date weights.
warnings.warn(msg)
Downloading: "https://download.pytorch.org/models/resnet101-63fe2227.pth" to /Users/ruangguru/.cache/torch/hub/checkpoints/resnet101-63fe2227.pth
100%|██████████| 171M/171M [06:37<00:00, 450kB/s] print(resnet)ResNet(
(conv1): Conv2d(3, 64, kernel_size=(7, 7), stride=(2, 2), padding=(3, 3), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(maxpool): MaxPool2d(kernel_size=3, stride=2, padding=1, dilation=1, ceil_mode=False)
(layer1): Sequential(
(0): Bottleneck(
(conv1): Conv2d(64, 64, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(downsample): Sequential(
(0): Conv2d(64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): Bottleneck(
(conv1): Conv2d(256, 64, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(2): Bottleneck(
(conv1): Conv2d(256, 64, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(64, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
)
(layer2): Sequential(
(0): Bottleneck(
(conv1): Conv2d(256, 128, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(downsample): Sequential(
(0): Conv2d(256, 512, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): Bottleneck(
(conv1): Conv2d(512, 128, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(2): Bottleneck(
(conv1): Conv2d(512, 128, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(3): Bottleneck(
(conv1): Conv2d(512, 128, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(128, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
)
(layer3): Sequential(
(0): Bottleneck(
(conv1): Conv2d(512, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(downsample): Sequential(
(0): Conv2d(512, 1024, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(2): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(3): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(4): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(5): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(6): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(7): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(8): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(9): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(10): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(11): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(12): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(13): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(14): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(15): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(16): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(17): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(18): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(19): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(20): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(21): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(22): Bottleneck(
(conv1): Conv2d(1024, 256, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(256, 1024, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(1024, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
)
(layer4): Sequential(
(0): Bottleneck(
(conv1): Conv2d(1024, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(512, 2048, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(2048, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
(downsample): Sequential(
(0): Conv2d(1024, 2048, kernel_size=(1, 1), stride=(2, 2), bias=False)
(1): BatchNorm2d(2048, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
)
)
(1): Bottleneck(
(conv1): Conv2d(2048, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(512, 2048, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(2048, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
(2): Bottleneck(
(conv1): Conv2d(2048, 512, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv2): Conv2d(512, 512, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
(bn2): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(conv3): Conv2d(512, 2048, kernel_size=(1, 1), stride=(1, 1), bias=False)
(bn3): BatchNorm2d(2048, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
(relu): ReLU(inplace=True)
)
)
(avgpool): AdaptiveAvgPool2d(output_size=(1, 1))
(fc): Linear(in_features=2048, out_features=1000, bias=True)
)Saving & Loading Models
Model that we have trained can be saved and loaded later. So that we don’t need to train it again.
Let’s try to save and load the model that we have trained before.
# save net model
torch.save(net, 'my_net.pkl')The saved file can be distributed to other people, or even deployed to production.
loaded_net = torch.load('my_net.pkl')
print(loaded_net)Net(
(layer_1): Linear(in_features=1, out_features=10, bias=True)
(layer_2): Linear(in_features=10, out_features=1, bias=True)
)